[Note: this quiz is due Wednesday, November 28th, at the beginning of class]

In this quiz you will get to play around with a mass spring system. First, you'll work out an expression for a spring force using the Lagrangian formulation we discussed in class. Next, you'll write a (very) short piece of code that implements this force, in an interactive JavaScript environment. If everything is working, you should see some nice bouncy shapes. (Don't forget to turn in your code!)

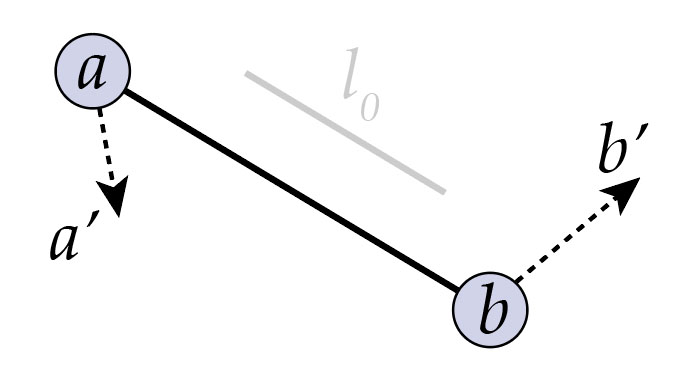
Task 1 - Derive the Spring Force

Consider a spring with endpoints a and b, a rest length l0, and a stiffness k. (For simplicity, we will assume that the mass of each particle is just m=1, and the spring itself has no mass.) We will use the method outlined on this slide to derive an expression for the spring force.

1a - Kinetic Energy

Write down an expression K for the kinetic energy of the spring in terms of the velocities a' and b' of the two endpoints. Check your work by making sure the quantity you've written down is a scalar, not a vector. (Hint: this is no different from the kinetic energy for a pair of particles not attached by a spring!)

1b - Potential Energy

Write down an expression U for the potential energy of the spring in terms of the positions a, b of the two endpoints, the stiffness k, and the rest length l0. You may use the internet (e.g., Wikipedia) if you forgot what the potential for a spring should look like. Check your work by making sure the quantity you've written down is a scalar, not a vector.

1c - Lagrangian

Write down an expression L for the Lagrangian of the spring.

1d - Euler-Lagrange equations

Next we will commpute the equations of motion. To make life simple, we will imagine that the endpoint b is fixed, and that only a is moving. Compute the following quantities:

• The partial derivative of L with respect to the position a.
• The partial derivative of L with respect to the velocity a'.
• The time derivative of the previous quantity.

All three quantities should be vectors, not scalars. Plug these quantities into the Euler-Lagrange equations (which you can find on this slide) to get the equations of motion for a. Repeat this calculation, now holding a fixed, to get the equations of motion for b. (This second calculation should be very similar, but not identical.)

1e - Final Forces

The Euler-Lagrange equations from the previous exercise basically give you an expression for "force equals mass times acceleration." What is the force F for each particle?

Task 2 - Use the Spring Force, Luke

Download this code skeleton (springthing.tar.gz) and open the file index.html. You should see a little mass spring system that currently falls through the floor. After writing (correct!) code, it should instead look like a little bouncy shape that you can toss around.

Open and edit the file particles.js. You should find a routine near line 210 called run(). Read the instructions inside this routine, and implement the TODOs. You should not need to write more than a few lines of code.

Print out your code and turn it in with your answers to Task 1 above.