In class we briefly brought up the question of how to detect collisions between two objects that are moving in time. Solving this problem exactly is already quite challenging for a pair of triangles (with new research on this seemingly basic question being published as recently as 2012!), so in this quiz we'll do what we know how to do best: start out simple, solve an easy problem, and build up additional complexity.
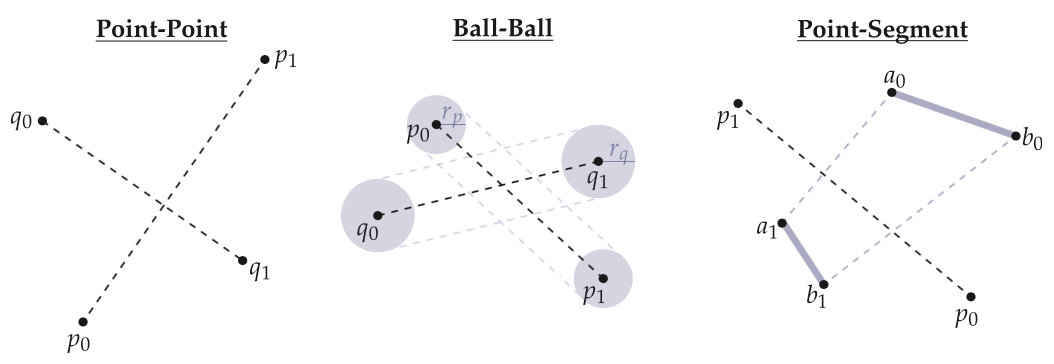
Question 1: Point-Point Intersection
Checking whether two points intersect is easy: just see if they have identical coordinates! But what if these points are moving? In particular, consider two points p, q in 2D moving along linear trajectories
p(t) = (1-t)p_0 + t p_1
and
q(t) = (1-t)q_0 + t q_1
over a time interval 0 <= t <= 1. How would you test whether these points bump into each-other? Describe your strategy explicitly: what quantities would you evaluate, and what tests would you perform, in terms of the variables t, p0, p1, q0, and q1.
Question 2: Ball-Ball Intersection
In reality, it's highly unlikely that two points will ever actually hit each other---imagine two particles of dust flying through deep space. However, as anyone who's ever played dodgeball knows, it is possible that two balls might hit each other mid-flight. Suppose in particular that our dodgeballs again have linear trajectories p(t) and q(t) in the interval 0 <= t <= 1 (exactly as above), but this time they have radii rp, rq > 0. How would you check if these two balls collide? Write out the equation(s) you would check, giving reasonably explicit expressions for how you'd compute the collision times t (if they exist). What are the possible interactions between the two balls, and how do they correspond to your equation(s)? [Hint: substitute complicated expressions for single variables when possible, in order to simplify your calculations.]
Quiz 3: Point-Segment Intersection
It's also possible that for a moving point to collide with a moving line segment---this test starts to be useful for, say, checking if two triangles collide. In particular, consider a point following a linear trajectory
p(t) = (1-t)p_0 + t p_1
and an edge with endpoints $a,b \in \mathbb{R}^2$ both following linear trajectories
a(t) = (1-t)a_0 + t a_1,
b(t) = (1-t)b_0 + t b_1,
all in the time interval 0 <= t <= 1. Setup an equation or equations you must solve to determine whether the point and the edge collide. This time you do not have to solve for $t$ explicitly; just give the equation that needs to be solved. However, you should comment on what kind of equation it is, and whether you think it can/cannot easily be solved.