Part of being a good developer is having some first-hand experience with the type of tools you're building. (It would be hard to become a great chef without occasionally tasting your own food!) So, in this quiz (and in the homework) you'll spend a little time exploring the artistic side of 3D modeling.

As mentioned in class, a very common paradigm in 3D modeling tools is box modeling: starting with a simple cube, one can create all sorts of interesting models by applying local mesh operations like bevels, edge flips, edge collapses, etc. (along with manipulation of the vertex positions). Although you are still in the process of building your first box modeler, this quiz will help you start to get a feel for box modeling.

Part I: Find a Tutorial / Demonstration / Cool Example

The first part of your assignment is to simply find a cool tutorial, or demonstration, or cool example of a mesh created using box modeling on the web and post a link to it in the comments of this slide. Your comment should also include an actual comment, i.e., you should say something that you learned from the tutorial, or why you found it interesting, or a question/idea that it brought up (e.g., "how did they suddenly get all those cool dragon scales at 2:13?"). (These resources will also help your classmates as you start thinking about the 3D modeling competition!)

Part II: Reverse Engineering a Box Model

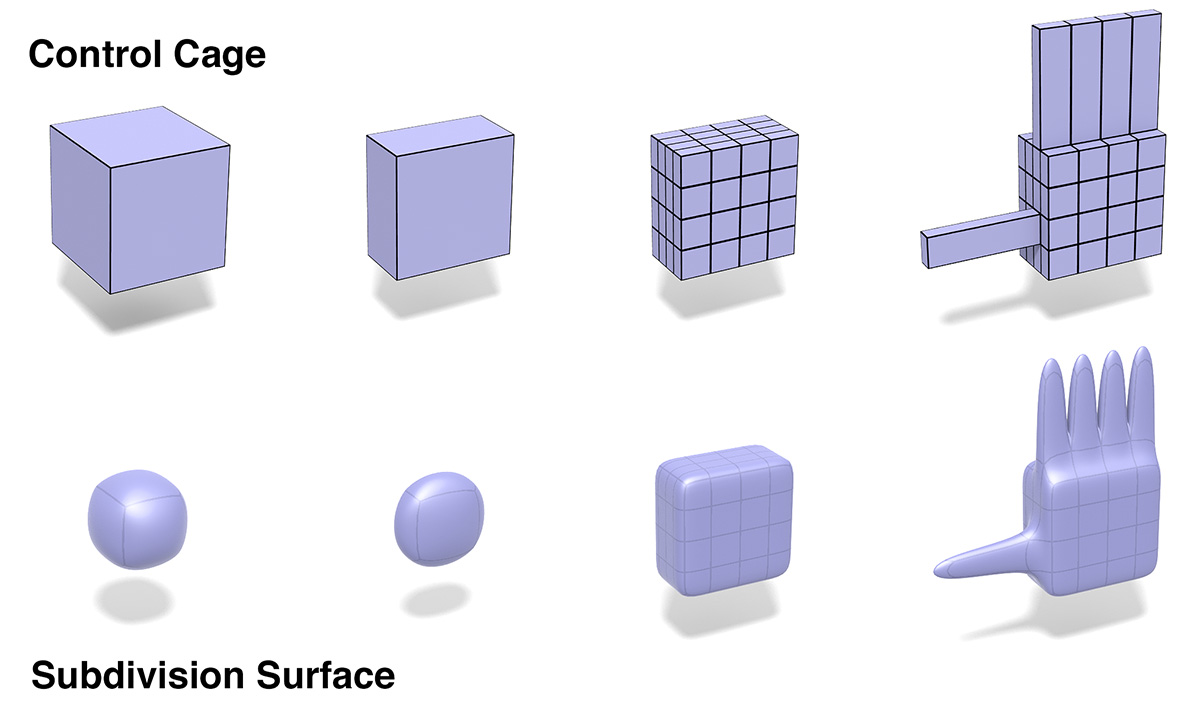
To learn from others' techniques, it is helpful to be able to "reverse engineer" how they achieved a particular model. I.e., looking at the final model, can you guess which operations (both geometric transformations and local mesh modifications) might have been used to create it? Below are two simple models that can be created using some basic local modeling operations (showing both the control cage and the subdivision surface at each step). Given the tutorials you looked at, and the modeling operations available in Scotty3D, how do you think each of these models might be achieved? Note that, unlike Scotty 3D, here we might operate on many elements at the same time. E.g., apply a bevel to all vertices, edges, or faces simultaneously, rather than one at a time. Describe each step in words, and turn in your answer on paper at the beginning of next class. (There of course may be more than one correct answer!)

Hand

(Number your steps H1 through H3)

Bug

(Number your steps B1 through B4)