In lecture, we discussed level set representations, which encode geometry as the zero set of a function stored on a grid. Often, we want to convert this implicit description to an explicit description (e.g., to make rendering easier).
In this case, suppose we have a 2D grid of values, which are positive outside the object and negative inside the object:
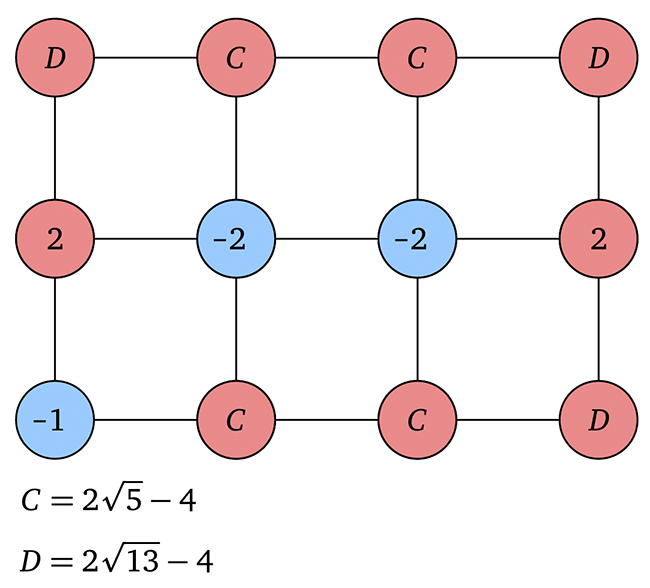
For simplicity, we will assume that each grid cell has dimensions 1x1. We now want to produce a collection of line segments that approximate the zero set. A simple observation we can make is that if we have a positive value a > 0 on one endpoint of an edge, and a negative value b < 0 at the other endpoint, then there must be a zero somewhere in the middle of the edge. So, to get an explicit description of our surface we can
- find the location of zeros along each edge that intersects the zero curve, and
- in each grid cell, connect zeros along line segments to get an explicit representation of this curve.
This algorithm is called "marching squares" (and in 3D there is an analogous algorithm called "marching cubes").
Question 1
If we use linear interpolation, along an edge with endpoint values a and b, where will we find the zero value?
Hint: write the linearly interpolated values as a function of t, which ranges between 0 and 1.
Question 2
Suppose now that we have a 4x3 grid with node values given in the picture above. Using your formula from the last part, find the zeros along each edge that intersects the curve. In each grid cell, connect these zeros along line segments to draw the final curve. (Are there any ambiguous cases?) Finally, fill in the "inside" of the curve. What shapes might these regions have been sampled from?
Hint: it's probably easiest to first compute the zeros in terms of c and d, then plug in the actual values at the end. (It's ok to use a calculator!)
Hint: try to take advantage of symmetry, so that you don't have to do so many calculations!
Solution:
(Question 1) The zero of the linear function can be found at t = a/(a-b); the surface will pass through this edge only if this t-value is between 0 and 1.
(Question 2) The values were sampled from the function
$4 \min\left(\sqrt{(x - 3/2)^2 + (y - 1)^2} - 1, \sqrt{(x - 1/4)^2 + y^2} - 1/2\right)$
i.e., the distance to a pair of circles. (The factor 4 is for convenience, and just makes the constants simpler to work with.)
There are two possible solutions: since every edge in the lower-left cell contains a zero, there are two different ways we can connect up the edges (without intersection). This kind of ambiguity is also a well-know problem with the marching cubes algorithm. One solution is to instead use the marching tetrahedra algorithm (or "marching triangles" in 2D).
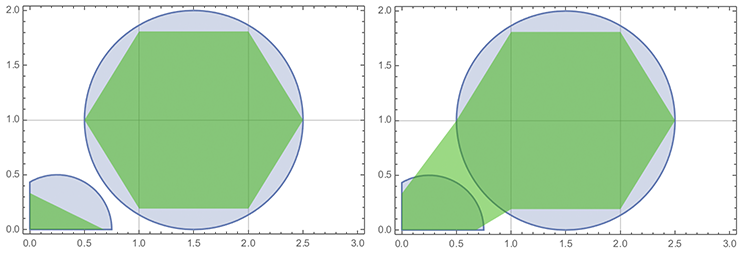
This outcome is yet another example of aliasing: because we only have a very small number of samples, the signal (or shape) we reconstruct can look very different from the one we sampled. In this case, we have not only geometric error (the reconstructed shape does not exaptly follow the circles), but also topological error (we might get one piece instead of two). On the whole, aliasing and sampling will become much more difficult (and interesting!) as we start to look at general geometric signals.