Question 1:

Slide 4 of the lecture illustrates all 64 basis images of the cosine basis (each basis image is an 8x8 image). The discrete cosine transform converts the representation of an image from its representation in the pixel basis (64 numbers corresponding to basis coefficients) to its representation in the cosine basis (another 64 numbers corresponding to basis coefficients). Note that we didn't explicitly talk about the "pixel basis" in class. Please describe the basis images of the pixel basis. (e.g., what does basis image (i,j) look like?)

Solution:

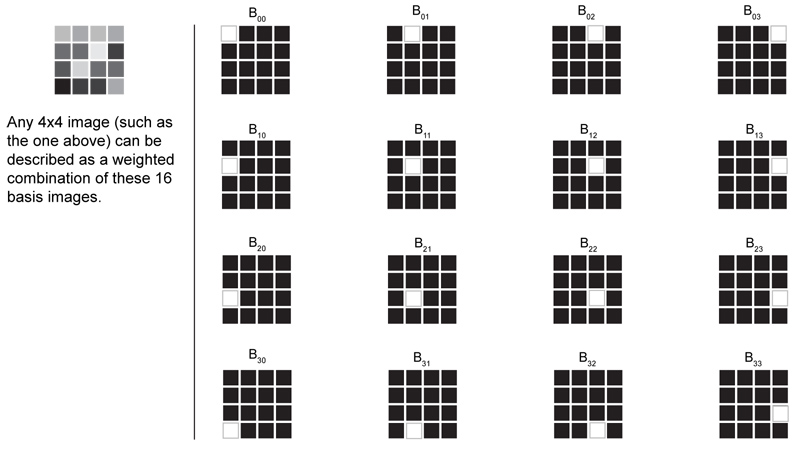
The "pixel basis" referred to in the question consists of a set of images where each image has a single pixel with full intensity, and all other pixels black. Therefore, any image can be thought of as a linear combination of all of these basis images. 16 images forming a basis for 4x4 pixel images is illustrated below. (keep in mind that a basis for 8x8 images, would require 64 basis images.)

Question 2:

In computer science, choosing the right representation for a task is often 90% of the challenge of solving a problem. In the example of JPEG compression, the goal is to achieve high compression ratios while minimizing the impact of this compression on image quality.

In the lecture we discussed two major representational choices used in JPEG compression:

• The decision to represent the color of pixels in Y'CbCr color space
• The decision to convert the representation of an image patch from the pixel basis to the cosine basis.

In each case, provide a reason why the chosen representation is very useful in the JPEG compression process.

Solution:

The use of the Y'CbCr color space represents color in terms of its lightness and its chroma. Since the human visual system is more sensitive to spatial variation in lightness, it is often acceptable to more aggressively compress chroma components of the representation than lightness. For example the 4:2:0 encoding of an image only stored chroma compoents at 1/2 resolution in the X and Y directions.

In JPEG compression, the representation of an image in the cosine basis makes it easy to reduce the accuracy of representation for high-frequency components of the image. the idea is that it is acceptiable to introduce compression errors in for these components, since the human visual system is less sensitive to these errors. After conversation to the cosine basis, the algorithm most aggressively quantized the coefficients of high frquency terms.