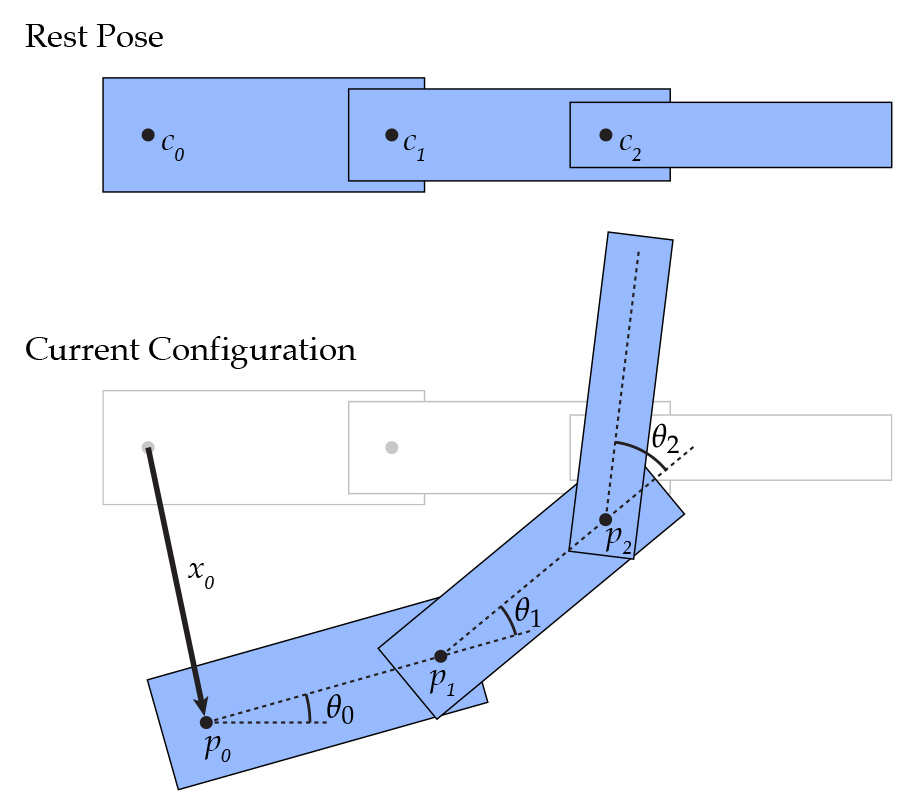
In your animation assignment, you will implement an inverse kinematics (IK) method that tries to move a particular joint center $c_k$ of your character toward a given goal point $q$ (usually the cursor) by adjusting the joint angles $\theta$ of the character. (Actually, you real code will be slightly more complicated because the user may want to click on some other point on the joint; not necessarily the center.) The character configuration is depicted below; in the original or "rest" pose, the centers sit at points $c_i$, and in the current or "deformed" configuration the centers sit at points $p_i$ whose position depends on the joint angles $\theta$ as well as a translation $x_0$ of the root joint.
IK optimization will be performed by running gradient descent on the objective
$$ f_0(\theta) = \tfrac{1}{2}| p_k(\theta) - q |^2 $$
Here $p_k(\theta)$ is the joint center $c_k$ transformed according to the current collection $\theta$ of all joint angles and the current translation $x_0$ of the root node. In particular, the transformed position $p_0$ of the root node is just
$$ p_0(\theta) = c_0 + x_0, $$
and the position of any other node $i$ is
$$ p_i(\theta) = p_j(\theta) + R(\theta_j)( c_i - c_j ), $$
where joint $j$ is the immediate parent of joint $i$, and $R(\theta_j)$ denotes a counter-clockwise rotation by the angle $\theta_j$. What do these equations say? The first one simply says that the current position of the root node is just the original position of the root node plus the current translation of the character. The second equation says that we can get the child's current position by taking the difference between its center and its parent's center, rotating it by the current joint angle, and adding it to the parent's current position.
The main challenge will be finding the gradient of this expression with respect to the joint angles. For instance, if the user rotates one of the angles $\theta_m$ a little bit, how much does the current position $p_n(\theta)$ of a given center change? Attacking this kind of problem is perhaps a bit challenging the first time you do it, but we have broken it down into several simple steps.
Question 1
Forgetting for the moment about the elaborate setup above, consider just a good old-fashioned function f(x) from the reals to the reals given by
$$ f(x) = \tfrac{1}{2}( x - c )^2 $$
where $c$ is a constant. What is the derivative of $f(x)$ with respect to $x$?
Question 2
Making things only slightly harder, suppose that $g(x)$ is another function of $x$. What is the derivative of
$$ f(x) = \tfrac{1}{2}( g(x) - c )^2 $$
with respect to $x$? You can express the solution in terms of the (unknown) derivative function $g^\prime(x)$.
Question 3
Here is a very different question. Suppose you have a vector $x = (x_1,x_2)$ and a vector $y = (y_1,y_2)$, and take their inner product $\langle x, y \rangle = x_1 y_1 + x_2 y_2$. Calculate the gradient of the inner product with respect to $x$
$$ \nabla_x \langle x, y \rangle, $$
i.e., the partial derivative $\partial/\partial x_1$ with respect to $x_1$, and the partial derivative $\partial/\partial x_2$ with respect to $x_2$, stuffed into a single vector. What is this vector? Can you express your result just in terms of the vectors $x$ and $y$ (rather than the individual components)?
Question 4
Combining the thinking from the previous questions, compute the gradient of the expression
$$ \tfrac{1}{2}| x - y |^2 $$
with respect to $x$. It might help to remember that the squared norm $|z|^2$ of any vector can be expressed as the inner product $\langle z, z \rangle$.
Question 5
Ok, now a purely geometric question. Suppose you have a bar of length $L$, rotating around the origin. How much length does the tip of the bar cover if it makes a full revolution of $2\pi$ radians? (Hint: the tip of the bar moves around in a circle.)
Question 6
Now that you know how far the tip of the bar moves over $2\pi$ radians, what is the distance it moves per radian? I.e., what is the rate of change of the position relative to the rate of change of the angle?
Question 7
Another geometric question: suppose you have a unit vector $u$ (remember that a unit vector is any vector of length 1: $|u|=1$). In particular, suppose that your unit vector is a function of time $u(t)$. At any given moment, you can ask , "how quickly is $u$ changing?" The change in the vector $u$ will be another vector, which we can call $\dot{u}$. In which direction must $\dot{u}$ point in order for $u$ to maintain its unit length over the course of time? (Hint: if it helps, you could try writing $u(t)$ as $(\cos(\phi(t)),\sin(\phi(t)))$ for some angle $\phi(t)$, and then take the derivative with respect to $t$. But it is much easier to just think about the geometry: what does the velocity vector look like for a point moving around in a circle?)
Question 8
Suppose that $u$ is not a unit vector, but can now have any length. What is the change in $u$ per radian? (The quantity describing the change must be a vector, of course, because $u$ is a vector.) All three of the previous questions will be helpful here.
Question 9
At this point, we have almost all the tools we need to take the derivative of our IK objective. The only piece remaining is: what is the derivative of $p_k(\theta)$ with respect to any particular angle $\theta_i$? Fortunately, this is a question we can answer without doing much calculation: we just have to reason about the geometry of the problem.
The first thing to notice is that $p_k$ will change only if $i$ is "further up the chain" from $k$. For instance, if $k$ is the arm and $i$ is a finger on that arm, changing the angle of the finger clearly doesn't change the position of the arm. Put more simply: you can bend your finger without changing the position of your elbow.
Next thing to notice: no matter how complicated the character is, and no matter how many joints are between $i$ and $k$, changing the angle $\theta_i$ a little bit will do one simple thing: it will rotate the position $p_k(\theta)$ around the point $p_i(\theta)$. Let's call the vector between these points $u$:
$$ u = p_i(\theta) - p_k(\theta). $$
We already know how a change in angle will affect a vector. We also know how to take the derivative of a function that looks like $\tfrac{1}{2}| x - y |^2$, and how to apply the chain rule to functions inside the square. Your job is to integrate all the knowledge you've gained above to come up with an expression for the derivative of $f_0$ with respect to a given angle $\theta_i$.