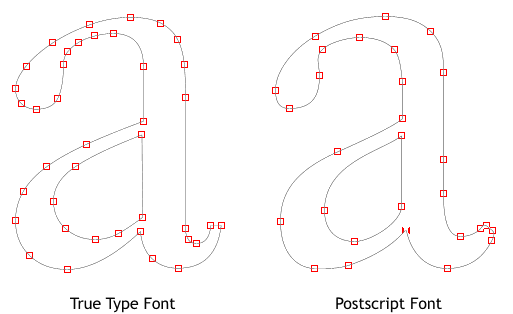
PostScript fonts are described by piecewise cubic curves, whereas TrueType fonts are described by piecewise quadratic curves. Converting from TrueType to PostScript is easy: every quadratic polynomial is also cubic. But converting from PostScript to TrueType is more challenging: we have to approximate our cubic curves by quadratic ones.

Question 1

Recall from our earlier lecture on geometry that a Bezier curve of any degree can be expressed in the Bernstein basis. Show that for a quadratic Bezier curve in the plane with control points (p,q,r), the tangents at the endpoints can be expressed as u = 2(q-p) and v = 2(r-q).

Question 2

In today's lecture we saw that for a cubic curve, we can exactly match a pair of endpoint locations and tangents at endpoints. For a quadratic curve we no longer have enough degrees of freedom to specify both tangents. Based on your answer above, can you still pick a middle point q that does a good job of approximating both tangents? Where would you put this point? Use your scheme to approximate the cubic "S" curve below as a pair of quadratic curves, indicating the control points for your quadratic curves and how they relate to the tangents. (You can simply draw a rough sketch of your approximation; it does not have to be exact.)