Question 1

Notice the difference in the shadows between the two photographs of Prof. Kayvon's hand shown below:

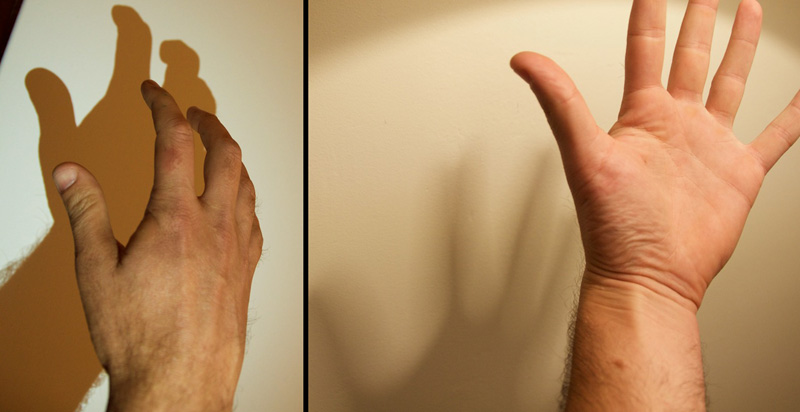
In the image at left, the hand casts a "hard shadow" edge. In the image at right, the shadow is much "fuzzier" (This effect is often called a "soft shadow" in computer graphics.)

• Describe the reason why the shadow in the left image has hard edges, and the shadow in the right image has much fuzzier boundaries. You're answer should not only describe the characteristics of the light sources that created these shadows, but also describe how these properties result in the effects shown in the picture.
• You'll notice that in the image at left, the shadowed region is not completely black. Give one potential reason why the wall is not completely dark even in regions where it is completely in the shadow of the hand.

Solution:

The shadow at left has hard edges because illumination is coming from a light source that is nearly a point source (in this case, it was the LED light on my iPhone). The entire light sources is either visible to most points on the wall receiving the shadow, or occluded by my hand. The shadow at right is soft because illuminations is coming from a much large area light source (in this case, a living room lamp, where light is emitted from all points on the lamp shade.)

The shadowed region in the photo is not completely black because the wall is illuminated by indirect illumination that arrives at the wall after reflection off some other surface in the room.

Question 2

Slide 41 leaves the derivation of uniform direction sampling of the hemisphere as an exercise to the students. Since you're a student, do the exercise! ;-)

Solution:

The gist of the solution is the following:

• We know that $p(\phi)$ is a constant, since any azimuthal angle is equally likely. Given a random number $\xi_2$ we can easily pick any $\phi = 2\pi\xi_2$.
• We also know that $dA \sim \sin \theta \mathrm{d}\theta \mathrm{d}\phi$, and that a uniform direction sampling is uniform area sampling of the hemisphere. So: $p(\phi, \theta) = C \sin \theta$
• Integrating $p(\phi, \theta)$ over the hemisphere gives $C=\frac{1}{2\pi}$.
• So $p(\phi,\theta) = \frac{1}{2\pi} \sin \theta = p(\theta)p(\phi)$ ($\phi$ and $\theta$ are independent variables)
• So $p(\theta) = \sin \theta$
• Integrating $p(\theta)$ yields $P(\theta) = -\cos \theta$
• Inverting the CDF yields: $\theta = \cos^{-1}\xi_1$ Done!