In class we discussed how to compute the irradience at point p on a plane due to incoming light from the surrounding environment. That computation is shown below. Please answer all questions asked in the figure below. In answering the "what is" parts of this question, try to describe the meaning of the quantity intuitively in your own words.
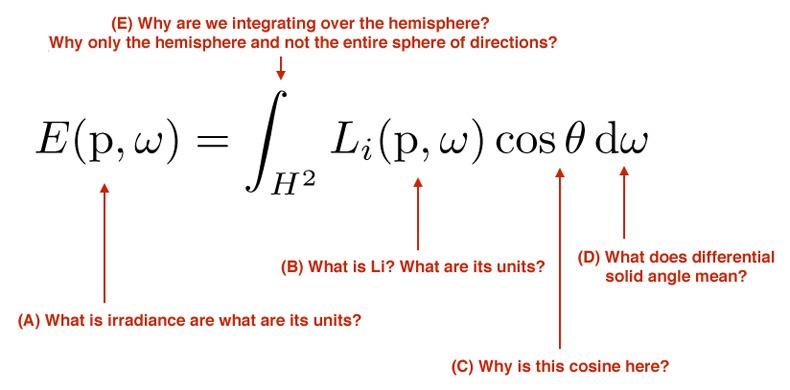
Solution:
(A) Irradiance is power per unit area. (Units: Watts/area)
(B) Li(p,w) is the incoming radiance reaching point P from direction w. Radiance is energy per unit area per unit angle, or in other words energy per infinitesimally small beam. (Another way to say it is energy carried along a ray.) Units: Watts/(area*steradian)
(C) The cosine in the equation is the conversion from radiance along w to incident differential irradiance on the surface. Radiance is power per unit sterian per unit area oriented normal to the beam, and irradiance is defined in terms of surface area. This is discussed in more detail here.
(D) This integral is integrating over all directions on the hemisphere. Differential solid angle is a tiny swath of the hemisphere. (An infinitesimal cone in a direction)
(E) We're integrating over the hemisphere about the normal of the surface. If we integrated over the engire sphere of directions, some of those directions would be pointing in the opposite direction from the surface (and since we're assuming the surface is opaque and exhibits no subsurface scattering) light from the back of the surface is never reflected off the front of it. Hence, the integral ignores these directions.