Question 1
$(A, B, C) = -(A, C, B)$ (Index Flip.)
Let the triangle be defined by the vertices $A$, $B$, and $C$.
Let $X = B - A$ and $Y = C - A$.
The Normal of the triangle is defined to be $N = X \times Y$.
If we were to perform the permutation $(A, B, C) \rightarrow (A, C, B)$, then the new normal value would be $N' = Y \times X$
Since the cross product is anticommutative, $N' = -N$, so this permutation negates the normal value.
$(A, B, C) = (C, A, B)$ (Cyclic Permutation.)
If we were to perform the permutation $(A, C, B) \rightarrow (C, A, B)$, then $X' = A-C = -Y$ and $Y' = B - C = X - Y$
The Normal is then $N'' = X' \times Y' = -Y \times (X - Y) = (-Y \times X) + (-Y) \times (-Y) = X \times Y + 0 = N$
Thus, the normal has been inverted again and is back to normal. <-- Pun ;-)
Via two non-cyclic permutations, we have thus proven that the cyclic permutation $(A, B, C) = (C, A, B)$.
Generality
We can then go on to assert that all cyclic permutations retain the same value by applying a cyclic permutation on the inputs to the proof above. We can also permute the values to derive any non-cyclic permutation. Hence, we have proven the desire properties for all permutations.
Question 2
Every triplet represents information about 1 face, 3 edges, and 3 vertices.
The key insight is that no two representations for a single edge may be in the identical order.
For instance, the face xbc cannot be consistently oriented with ybc, cyb, or bcy.
On the other hand the face xbc is consistently oriented with ycb, byc, or cby.
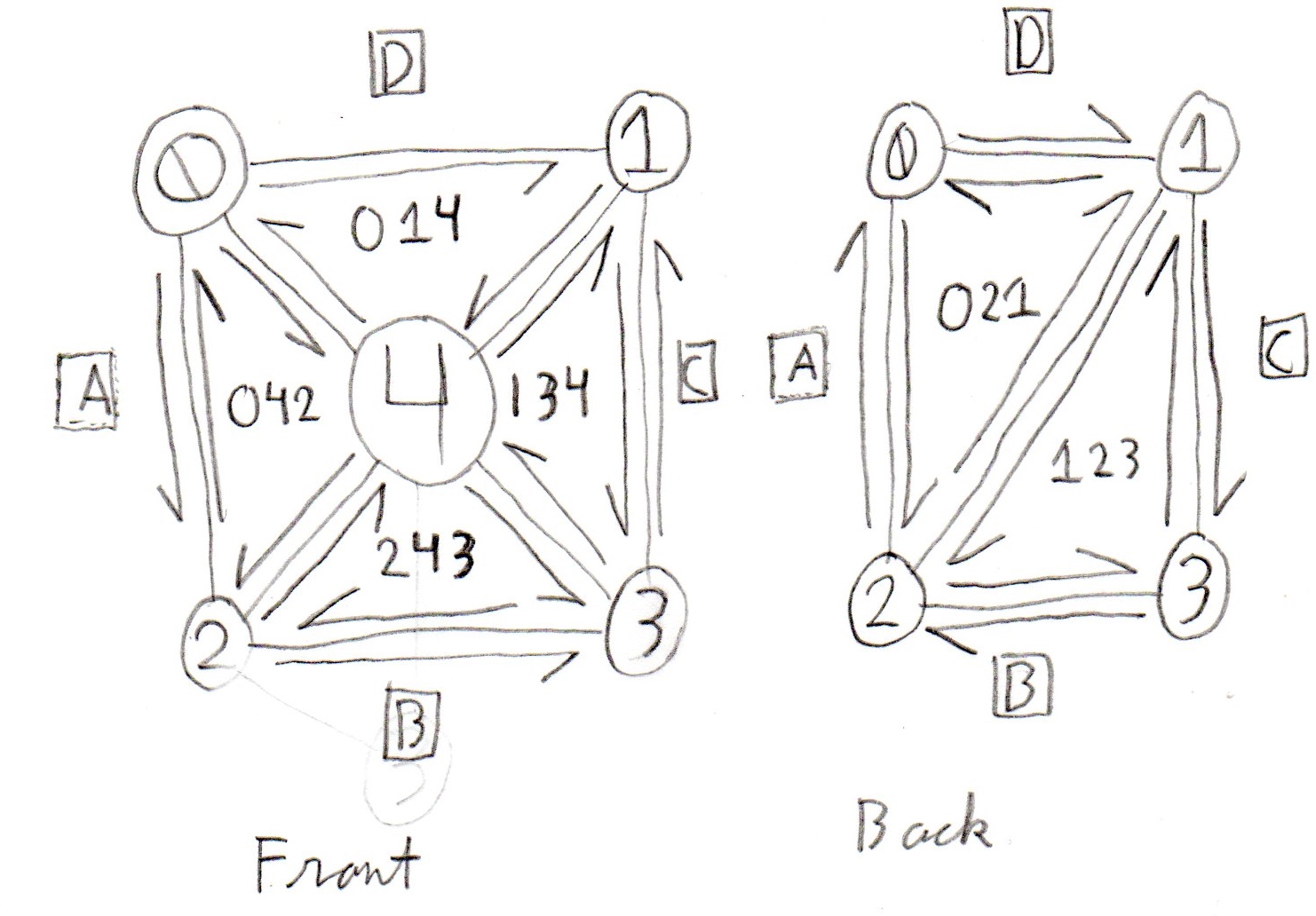
Mesh 1
Here is an illustration of a consistent orientation for Mesh 1, which looks like a rectangular pyramid. Please Note that locally all triangles have the same clockwise-ness.
Mesh 2
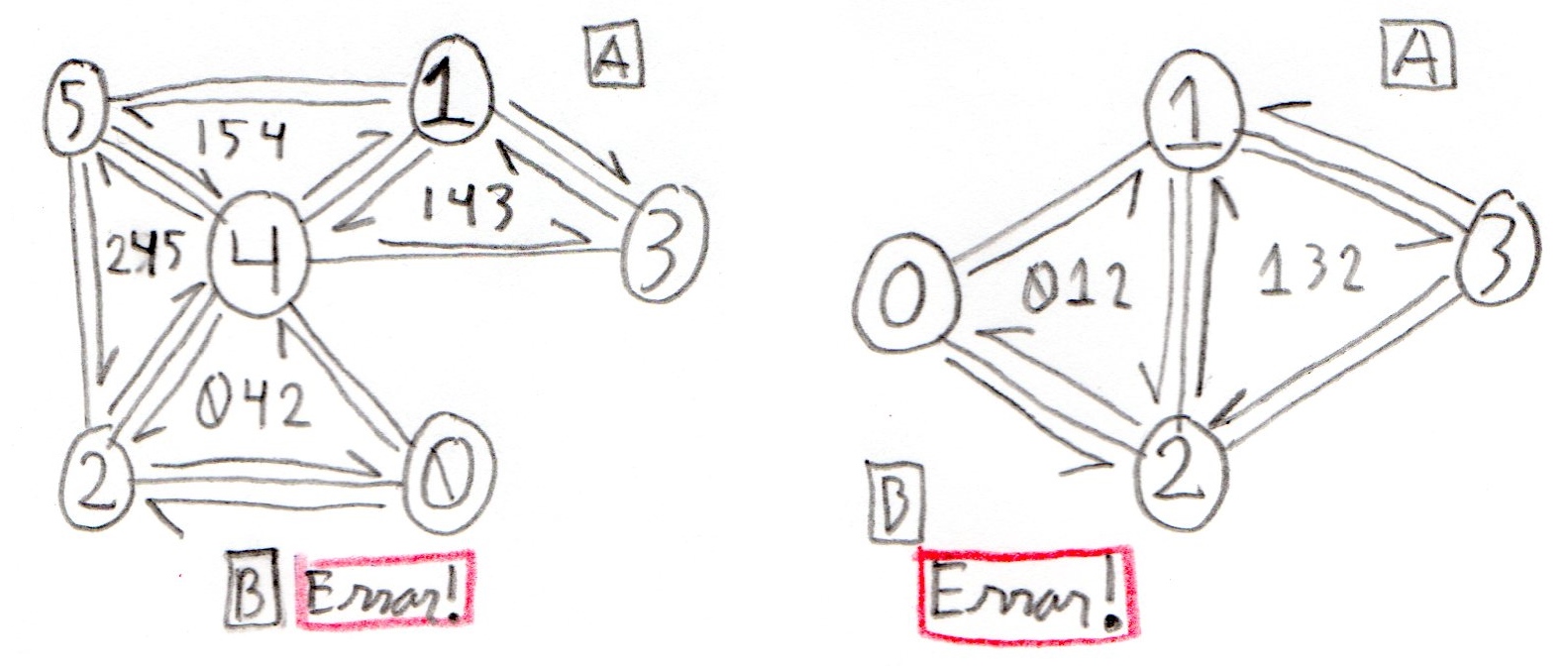
Mesh 2 looks kind of like a lopsided Hexagon with 2 extra faces (012 and 132).
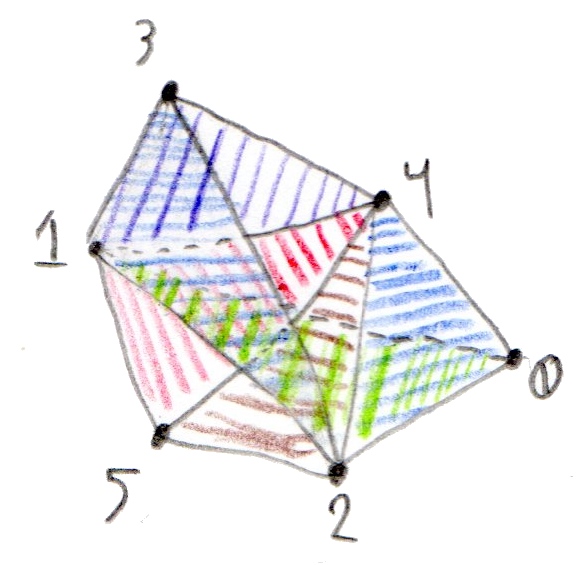
Here is an illustration showing the faces of Mesh 2. Please note that it is actually impossible to consistently orient mesh 2, because it is a triangulation of a Mobius band. To see this, please take a good look at half edges (0, 2) and (2, 0).
Question 3
The requirements for manifold edges and vertices are discussed on this slide
- An Edge is manifold if it is contained in at most 2 faces.
- An Edge is not manifold if it is contained in more than 2 faces.
- An Edge is on a boundary if and only if it is contained in exactly 1 face.
- A Vertex is manifold if and only if its neighbors form a closed loop.
- A Vertex is on the boundary if at least 2 of its incident edges are on the boundary.
- A Vertex non manifold if its neighbors do not form a loop.
To answer question 3, we could draw a picture, but it could lead us to unjustified conclusions if we are not careful to indicate which faces exist and which ones are merely implied by the illustration. When in doubt trust the original data, rather than a picture.
We can derive the states of all of the edges by creating an edge frequency table without the need for a picture.
| Edge Name | Frequency | Classification |
|---|---|---|
| 0, 1 | 1 | Boundary |
| 0, 2 | 1 | Boundary |
| 0, 5 | 2 | Manifold |
| 1, 2 | 1 | Boundary |
| 1, 5 | 2 | Manifold |
| 2, 5 | 2 | Manifold |
| 3, 4 | 3 | Non-Manifold |
| 3, 5 | 2 | Manifold |
| 3, 6 | 1 | Boundary |
| 3, 7 | 1 | Boundary |
| 3, 10 | 1 | Boundary |
| 4, 5 | 2 | Manifold |
| 4, 6 | 1 | Boundary |
| 4, 7 | 1 | Boundary |
| 4, 10 | 1 | Boundary |
| 5, 10 | 2 | Manifold |
| 8, 9 | 1 | Boundary |
| 8, 10 | 1 | Boundary |
| 9, 10 | 1 | Boundary |
| ---------- | ----------- | --------------- |
For the vertices, we could use some nifty algorithms and numerical observations for detecting loops purely based on the edges, but it is probably more convenient to draw a careful illustration. Notice the non-existence of faces (0,1,2) and (3,4,10).
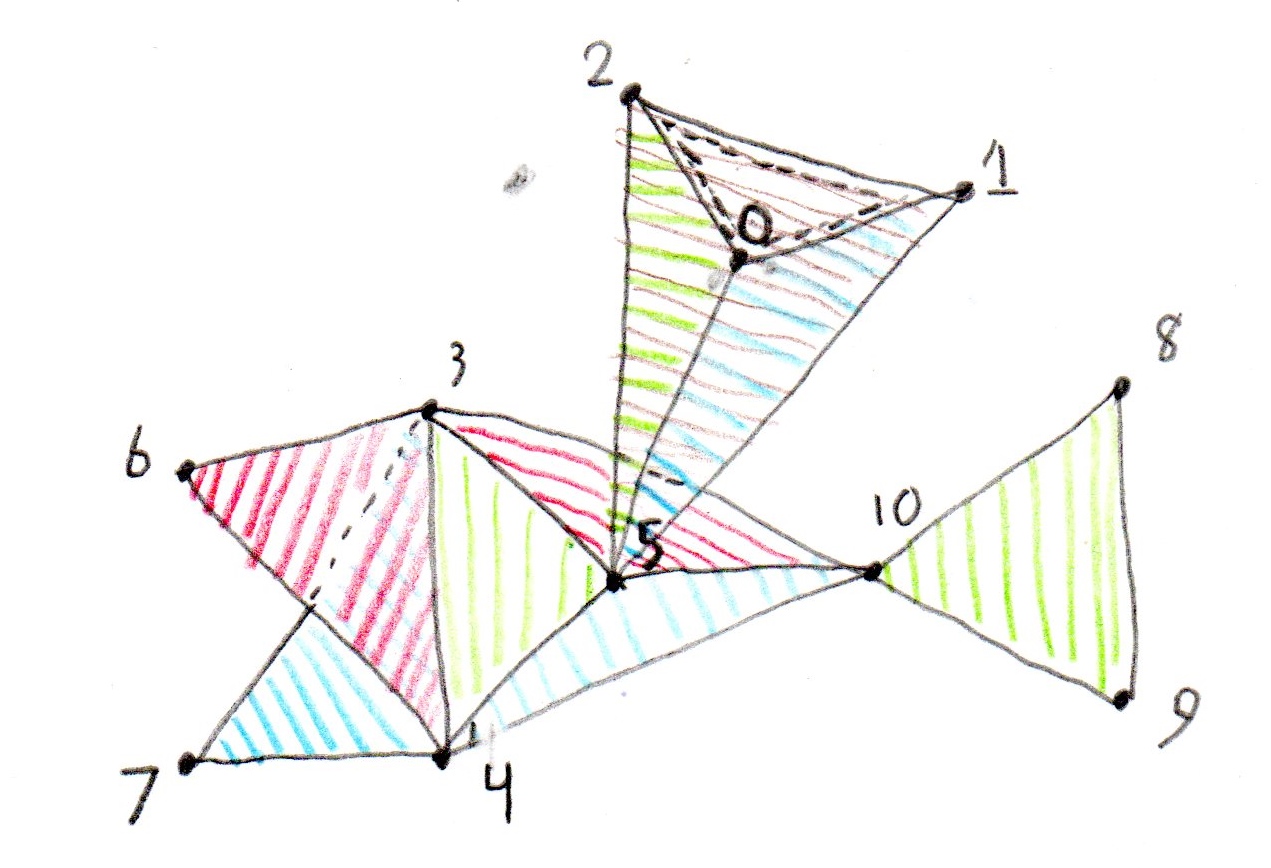
By Looking at our illustration, we can visually see which vertices do not have a canonical single open/closed loop by looking at the neighborhoods of each vertex. Here is an illustration of the neighborhoods of non-manifold vertices 3, 4, 5, and 10. Please notice that they each have 2 different potential loops indicated in red and green. Blue is used to indicate the "fan artery" edges that define the neighborhood.
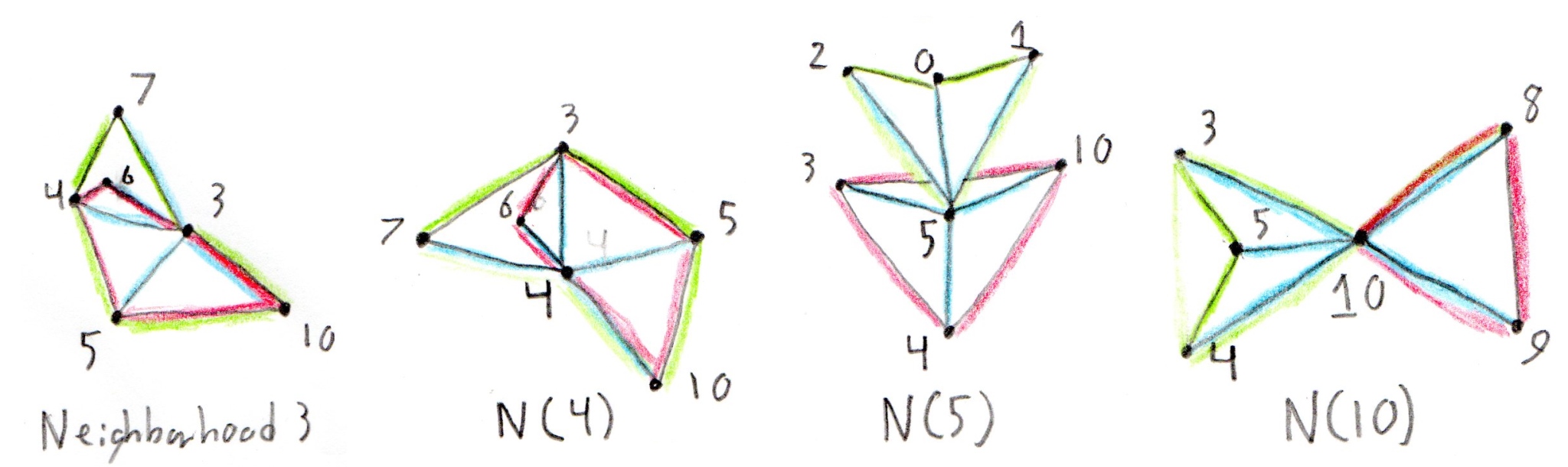
The other vertices in the mesh have well behaved neighborhoods and are therefore manifold. Several of them are also on the boundary, namely 6, 7, 8, and 9.
This leads us to the following classification chart for all of the vertices.
| Vertex Name | Classification |
|---|---|
| 0 | Boundary |
| 1 | Boundary |
| 2 | Boundary |
| 3 | Non-Manifold |
| 4 | Non-Manifold |
| 5 | Non-Manifold |
| 6 | Boundary |
| 7 | Boundary |
| 8 | Boundary |
| 9 | Boundary |
| 10 | Non-Manifold |
| ------------ | -------------- |