In this course, we will be representing all of our geometry in terms of a halfedge mesh. The basic idea behind the halfedge data structure is that, in addition to the usual vertices, edges, and faces that make up a polygonal mesh, we also have an entity called a halfedge that acts like "glue" connecting the different elements. It is this glue that allow us to easily "navigate" the mesh, i.e., easily access mesh elements adjacent to a given element.

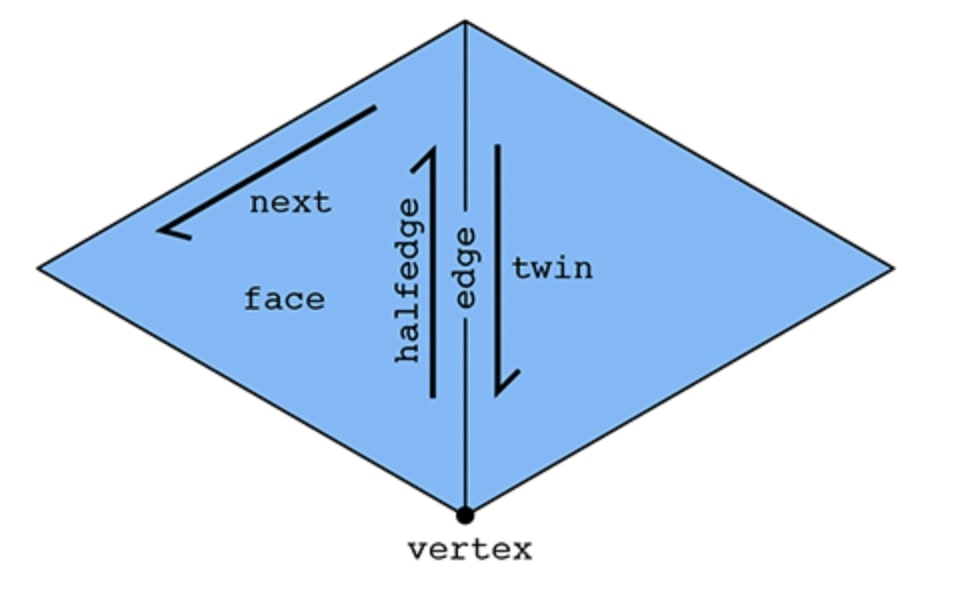
In particular, there are two halfedges associated with each edge (see picture above). For an edge connecting two vertices i and j, one of its halfedges points from i to j; the other one points from j to i. In other words, we say that the two halfedges are oppositely oriented. On of the halfedges is associated with the face to the "left" of the edge; the other is associated with the face to the "right." Each halfedge knows about the opposite halfedge, which we call its twin. It also knows about the next halfedge around its face, as well as its associated edge, face, and vertex.

In contrast, the standard mesh elements (vertices, edges, and faces) know only about one of their halfedges. In particular:

• a vertex knows about one of its "outgoing" halfedges,
• an edge knows about one of its two halfedges, and
• a face knows about one of the many halfedges circulating around its interior. We can use these relationships to traverse from any mesh element to any other. For example, in the above mesh, we can go around the triangle by calling halfedge->next()->next(). We can get the vertex by doing halfedge->vertex().

Questions

You may wish to review how halfedge meshes with boundary are represented in Scotty3D.

Then consider the following mesh. The face 'b' represents the boundary of the mesh.

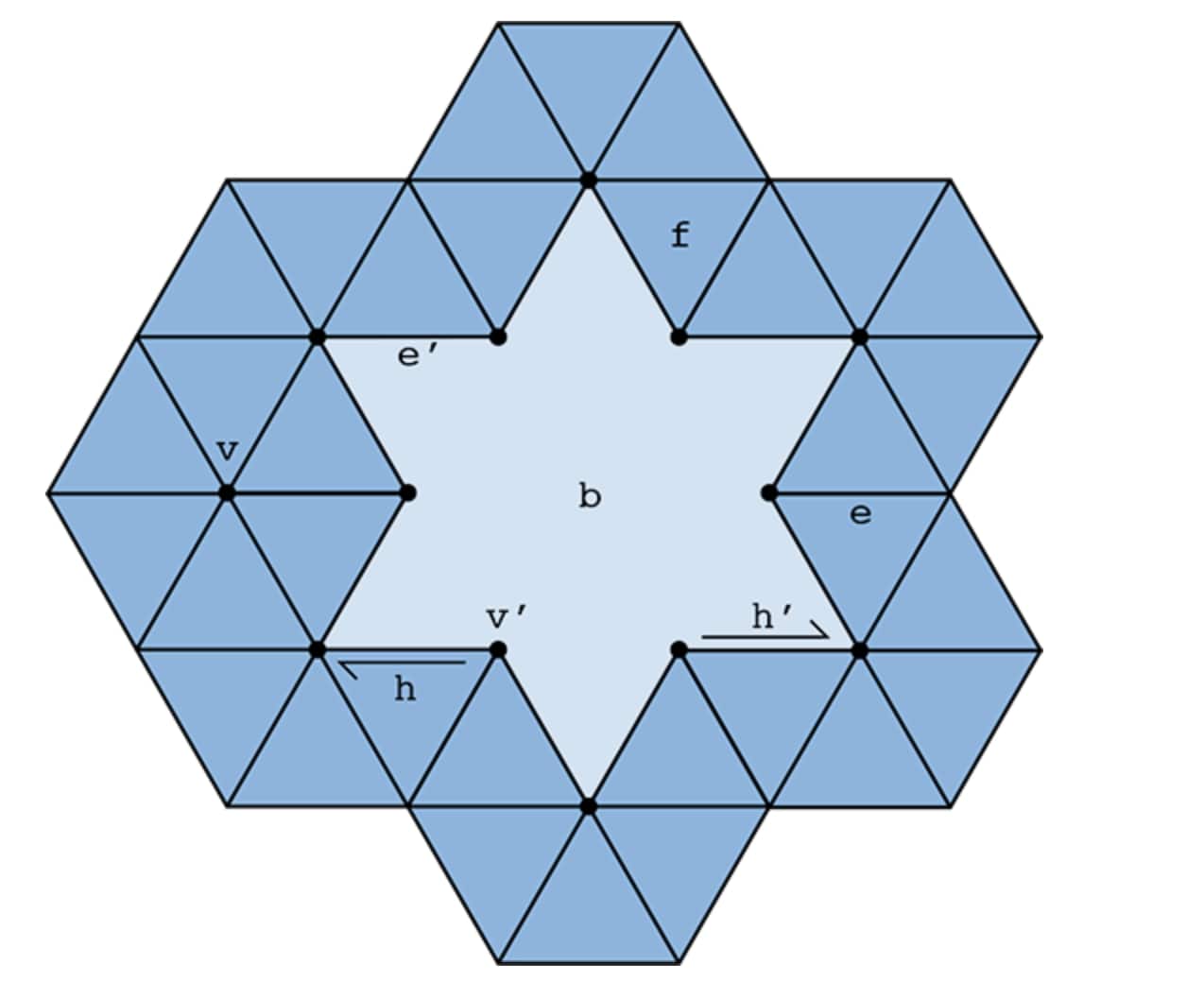
Question 1

Describe a path from h to h' using the notation in the above paragraph. What is the length of the shortest number of operations from h to f? (For reference, h->next()->face() counts as 2 ops.)

Question 2

First review the local mesh operations supported by Scotty3D. You can also see them in action here.

What is a local operation that does not make sense to apply to e', and why? Describe a mesh without boundary in which some local operation would not make sense to apply.

Question 3

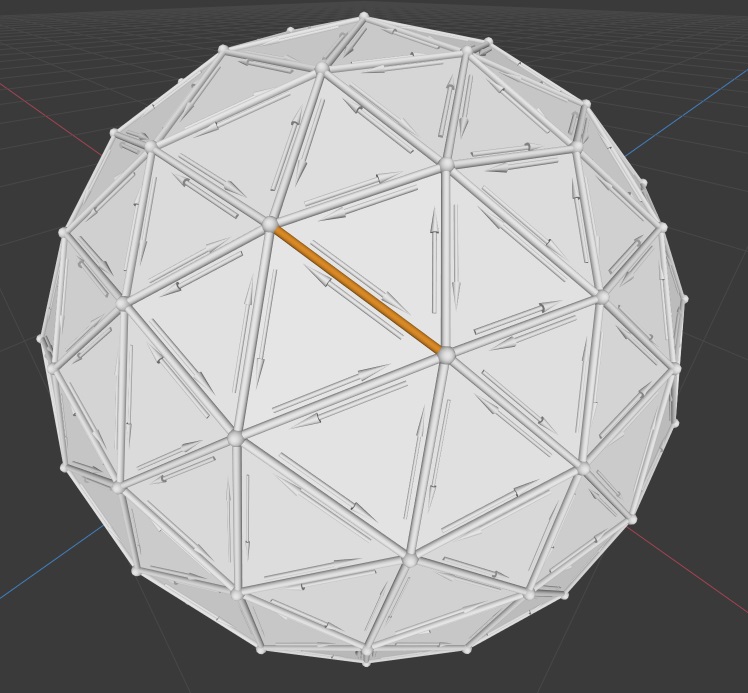
Starting from the selected edge, this mesh has had two local operations applied to it. What were they?