Continuous Probability

This miniHomework is all about probability, and we hope it prepares you for the environmental lighting portion of A3. We will cover basic concepts such as probability density functions, probability mass functions, and different sampling techniques.

Part 1: PDFs and PMFs

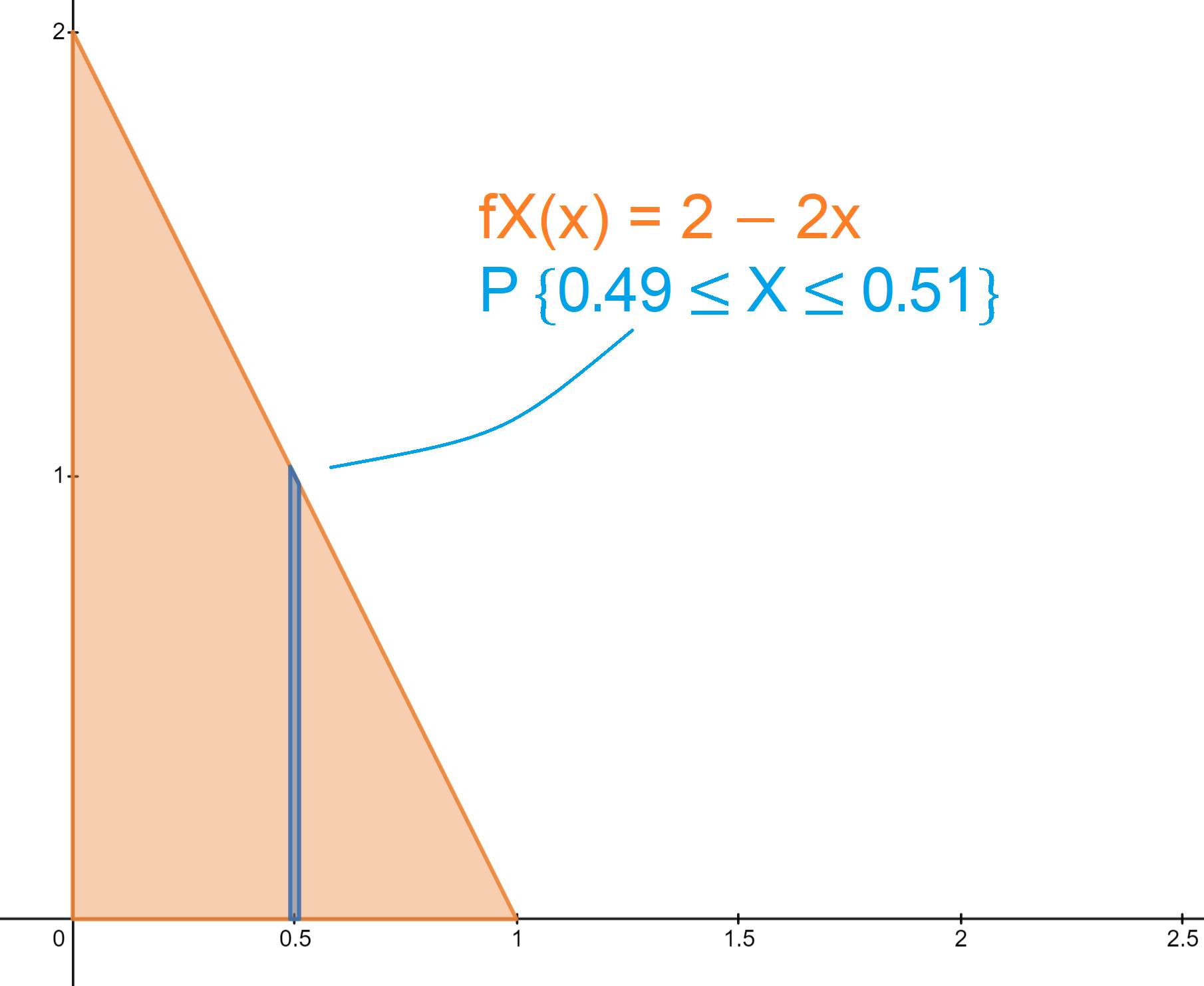
Please read section 1 in this handout, and complete all questions in section 1.1. We have provided you with supplementary diagrams that will hopefully aid you in solving the problem.

Part 2: Sampling Techniques

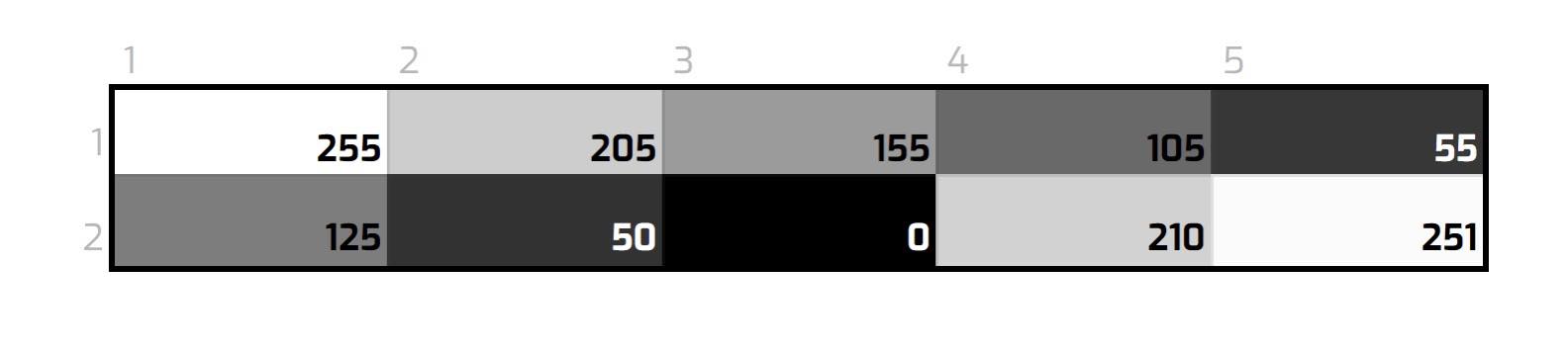
Please read section 2 in this handout, and consider the following question: Consider that you want to perform inverse sampling on a 10-pixel monochrome image that's your environment map, provided below. This image is stored in a 2D vector of [2][5]. If you do uniform sampling, each pixel has a 1/10th chance of getting sampled. However, you want to perform importance sampling, such that the probability of a pixel getting sampled is proportional to its brightness/luminance. How would you do that?

1. Please write a function int f(vector<vector\<int>> image), a function that takes in the image, and returns the value of a pixel sampled using importance sampling. You may define any additional data structure you want in this function, and you're allowed to assume the image array is always going to be 2*5. (If you don't have an idea on how to start, take a look at the recitation slides on importance sampling!)

2. Comparing inversion sampling and rejection sampling, which of these methods might require more computation, and which might require more random numbers?