This mini-homework will get you a bit more familiar with spacial data structures, which is covered on Wednesday's lecture.
Part 1
 Suppose you wanted to ray trace each of the scenes above (assuming they were each nicely represented as a triangle mesh). What spatial acceleration data structures would make sense, and why? You could use just a single structure, or a combination of several structures we saw in class (BVH, kd-tree, regular grid, octree). Since there are many possibilities here, we will mostly be focusing on your answer to the "why" question! (And will give full credit as long as you give a reasonable justification.)
Suppose you wanted to ray trace each of the scenes above (assuming they were each nicely represented as a triangle mesh). What spatial acceleration data structures would make sense, and why? You could use just a single structure, or a combination of several structures we saw in class (BVH, kd-tree, regular grid, octree). Since there are many possibilities here, we will mostly be focusing on your answer to the "why" question! (And will give full credit as long as you give a reasonable justification.)
Part 2
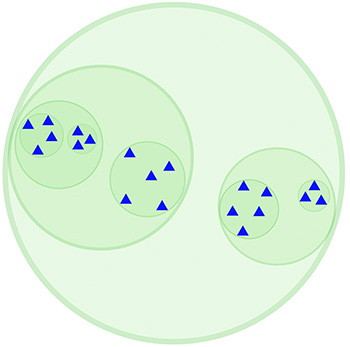
In class, we spent all of our time talking about how to accelerate ray-intersection queries using spatial acceleration data structures. But can we use the same hierarchical strategy for other types of geometric queries? Suppose, for instance, that given a query point p I want to find the closest point on a collection of primitives (triangles, say). Moreover, suppose that instead of bounding boxes, I now have bounding spheres. The data structure for my bounding sphere hierarchy is
struct BSHNode
{
bool isLeaf; // true if this node is a leaf node; false otherwise
Vector3D center; // center of the bounding sphere
double radius; // radius of the bounding sphere
BSHNode* child1; // left child (NULL for leaf node)
BSHNode* child2; // right child (NULL for leaf node)
int nPrimitives; // number of primitives (unused for internal nodes)
Primitive* primitives; // list of primitives (NULL for internal nodes)
}Like our BVH, each node of the BSH (bounding sphere hierarchy) is either a leaf, storing a collection of primitives, or an interior node, pointing to two children. Each node also describes a sphere that tightly fits around all the primitives contained in itself or its two sub-trees.
Your task is to implement a method that computes the smallest distance to all primitives contained inside a given node:
void distance( BSHNode* n, // node of interest
Vector3D p, // query point
double* d ) // smallest distance seen so far
{
// TODO: update d
}This method will be called on the root node, with an initial distance d of "infinity". You may assume that each primitive has a method primitive.distance(p) which returns the distance to the closest point on that primitive to the given point p. Full credit will be given for an algorithm that is asymptotically optimal (e.g., you will not get full points for just checking all the primitives in the entire tree!). Think carefully about when you can and cannot skip a child node. You will also need to think about how to measure the distance from a point p to a sphere (hopefully this should not be too hard! :-))
Our slide outlining the basic algorithm for BVH traversal is a good starting point, but be careful not to just copy this algorithm verbatim! Things will work slightly differently for the closest point query. Note that this routine is slightly simpler than the ray intersection routine since we are only interested in the closest distance; we do not care which primitive is closest.
Part 3
![]()
![]()
Now that you've seen closest point queries and ray-intersection queries, for the two scenes above, which one is likely to explore more nodes in a BVH? Why? (Image credits: dataset)