[This quiz is due at the beginning of class on Wednesday, April 29th. It will give you some exposure to inverse kinematics (IK), even though we're not requiring you implement IK for A4. It's also the last quiz of the semester. Congrats! You made it! :-)]

For this quiz, you will be implementing an optimization algorithm known as gradient descent. As implied by the name, this is an optimization algorithm that allows you to 'ski down' a function until you reach one of its (local) minima. Gradient descent, in various forms, is broadly used not only in computer graphics, but also machine learning, robotics, and much much more. In your animation assignment, you will use gradient descent to implement inverse kinematics (IK). For now, let's start with the much simpler problem of finding minima of an ordinary function of one variable.

Assume we have a function F(x), and want to find the value of x for which F(x) is equal to some target value y. In practice, it is often good enough to find a value of x for which F(x) is numerically very, very close to y. (In IK, for instance, y will represent the desired location for our end-effector, and F(x) will give the position of the joints as a function of the joint angles.) Trying to get F(x) close to y can be done by minimizing the error f(x) = ||F(x) - y||. The basic idea of gradient descent is as follows:

while (cost is high)
{
   // Compute derivative of f(x) at current x
   u = gradF(x)

   // Move toward minimum
   x = x - u * stepSize

   // Recompute cost function based on new X
   cost = F(x)
}

Part 1a

Download the given code (gradientdescent.tar.gz) and take a look at the TODOs in optimize.js. You will implement code for a function that performs one iteration of gradient descent, and evaluates the cost function. Once you have written this code, you will be able to load index.html in your browser and visualize the gradient descent process.

We will try to find the closest point between the function F(x) given by

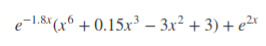
and the target value y = 3.4. We will use the cost function

f(x) = (F(x)-y)^2/2.

Compute the derivative in terms of the function F(x), and implement it in the code above. Please complete and turn in the relevant code you wrote for this part.

Part 1b

There are several parameters to tune here, such as tolerance (how small does our cost function to converge?), step size (how large of a step in the negative direction of the gradient are we taking?) and initial starting position for the optimization. Visualize gradient descent for different parameter settings and suggest some problems and pitfalls you might run into with this simple algorithm.

Part 2

In inverse kinematics, we want to select a target joint and an arbitrary point in space and have the joints move in such a way that the target joint is as close to our desired point as possible. The change in position of our target joint for a small change in joint angle can be estimated as:

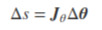
i.e., the change in position is a function of the product of the Jacobian and the change in joint angles. The Jacobian is an generalization of usual first-order derivatives, which describes all the first-order derivatives of a vector-valued function. It can be defined as:

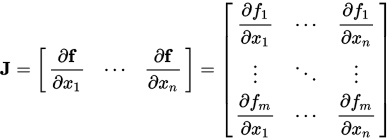
Briefly try to explain what the Jacobian means in the context of inverse kinematics.