Note that this homework requires a lot of thinking and computation, so please start early! Our goal here is to get you thinking deeply about how color works, and how that interacts with linear algebra. This is how real-world graphics problems often look: they get quite messy! So, we will be generously giving partial credit for earnest attempts. Tasks 5 and 6 are extra credit.
(Task 0): Start by familiarizing yourself with Among Us, and consider joining us Fridays at 9pm EST on Discord for game night!

You're walking alone in Electrical when you notice the body of one of your crewmates in front of you. For a moment, you see another crewmate of a different color suit stand next to the body before quickly retreating into the vents. You are barely able to pick out the color of the imposter, but your suit is equipped with a high-tech colorimeter, built from a synthetic human retina (!), that is able to measure the SML values of the suit.
The SML values you detect are (s', m', l') = (0.00, 0.48, 0.27). It would be easy to know the true color of the impostor if it hadn't been for the fact that the lights in electrical have been acting up recently and have changed color. If only you knew the color of the lights...
Fortunately, you also measured the color (s0,m0,l0) = (1.7,15.0,11.6) of your own suit, which you can use to calibrate the lighting. The lights in electrical consist of a strip of red, green, and blue LED lights, each with a corresponding intensity. You need to find these intensities in order to determine the overall color of the light in Electrical. We'll consider the following data:
Scalars:
r,g,b - unknown intensity of red, green, and blue lights
s',m',l' - observed SML intensities of imposter's suit under colored lighting
s0,m0,l0 - observed SML intensities of your own suit under colored lighting
Functions of wavelength λ:
R (λ) — known emittance of red light bulb
G (λ) — known emittance of green light bulb
B (λ) — known emittance of blue light bulb
S (λ) — known response curve of short cone
M (λ) — known response curve of medium cone
L (λ) — known response curve of long cone
A (λ) — known absorption of your own suit (between 0 and 1)
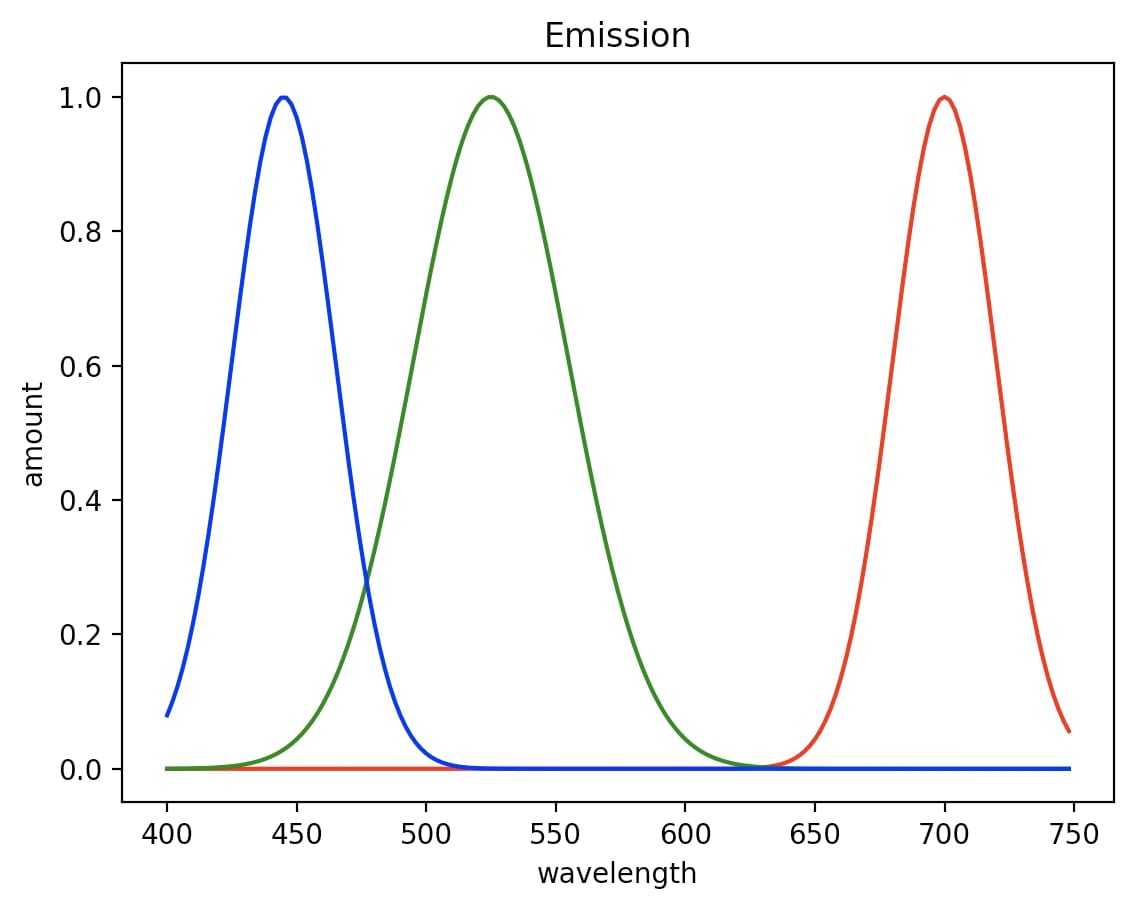
You might be wondering why R(λ), G(λ), B(λ) are functions of wavelength and not just constant intensities. The reason is that real LED lightbulb emits a range of wavelengths centered around their main wavelength. So while red, green and blue have wavelengths λr = 700nm, λg = 525nm, and λb = 445nm, we'll assume the LED light bulbs emit additional wavelengths in a Gaussian distribution centered around these values:
Your task is to determine the scalar intensities of the lights at the moment you saw the imposter. You want to find intensity values (r,g,b) for the lights such that the colors (s,m,l) predicted by your model are as close as possible to the (s0, m0, l0) values you observed from your own suit.
(Task 1): Write an expression for the predicted s, m, and l intensities for your own suit as a function of the three light intensities r, g, b. Rather than writing everything out in individual scalar components, you should keep your expressions concise by using the following 3x1 vector quantities:
x = [r g b]T — the intensities of the three lights
s = [s(r) s(g) s(b)]T — the total stimulation of short (S) cones due to each light
m = [m(r) m(g) m(b)]T — the total stimulation of medium (M) cones due to each light
l = [l(r) l(g) l(b)]T — the total stimulation of long (L) cones due to each light
Your expressions should end up using the absorption spectrum A of your own suit, the emission spectra of the three lights R, G, B, and the response curves S, M, L, but the final values s(r), s(g), s(b), etc., should each be scalars. For this task, assume that R, G, B, S, M, L, and A are all continuous functions (hence your answer may involves some integrals).
It is helpful to remember that a dot product can be written using the transpose, i.e., for any two vectors u and v,
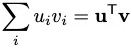
You can therefore write the final scalar (s, m, l) intensities as:
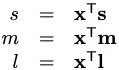
To make this task easier, you should break it down into one small step at a time. For instance, just try to write s(r) first, which is a scalar giving the stimulation of the S cones due to the red light, as a function of the red light's intensity r. Think about all the factors that contribute to this quantity: the emissivity of the red light; the amount of light reflected by your suit; and the response of the S cones themselves. What is the response for a single frequency λ? How do you get the total response over all frequencies λ?
Hint: how can you approximate the integrals your wrote down in Task 1? Think about the relationship between the Euclidean inner product and the L2 inner product that we discussed in our linear algebra review.
(Task 2): To estimate the light intensities x = [r, g, b]T observed in Electrical, you'll want to minimize the difference between the predicted color of your suit under colored illumination, and the values you actually measured:
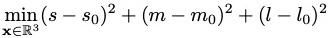
To find the minimum, we'll want to re-write this problem in matrix notation:
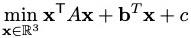
For this task, you must give the 3x3 matrix A, the 3x1 vector b, and the scalar c. Your final expression should involve the vectors s, m, l, x, and the scalars s0, m0, l0.
Hint: if you think of a scalar a as a 1x1 matrix, then its square can be written as a2 = aTa.
(Task 3): Write down an expression for the vector x that minimizes xT A x + bTx + c, in terms of just the quantities A, b, and c. (Do not expand these expressions in terms of the data from the previous tasks.) Explain why, for this problem, the solution you give corresponds to a minimum rather than a maximum or saddle point.
Hint: as in ordinary calculus, finding the minimizer boils down to setting the derivative to zero and solving for x. The video/slides on minimizing a quadratic polynomial will be very helpful here.
(Task 4): Numerically solve for the minimized x using the equations you wrote in Tasks 1-3. Describe the resulting light color in English (hint: it's a common color!). You'll want to use the data files and starter code here, which is in Python.
You will find it helpful to use functions from NumPy, which is a standard Python library for numerical linear algebra. See especially the help pages for NumPy arrays (which can be used to build both matrices and vectors), the dot function (which can be used for dot products and matrix-vector multiplication), and the method for solving a linear system (which should be used instead of "inverse", since the systems you want to solve are pretty badly conditioned!).
(Task 5) Ok, great. We now know the intensity of the red, green, and blue lights at the time we took the SML measurement of the impostor. Now we want to find out what the impostor would look like under an ordinary, white light. For simplicity, we'll assume that "white light" means that all three lights have equal intensity, i.e., r=g=b=1. How can you get a rough estimate of what color the impostor looked like under white light, in the RGB color space? Use c [cr, cg, cb]T to denote the red, green, and blue components of your estimated color. (Hint: try modeling the reflection spectrum of the imposter's material as isolated "spikes" in the peak frequencies of the red, green, and blue LED lights.)
(Task 6): Suddenly, your friend on Discord tells you that they were in security and saw the color of the suit. "It's purple! I saw purple vent!", they say. But you know better---you've carefully approximated the true color (under white lights), in Task 5. Who was the real impostor, i.e., what color does your RGB color correspond to in English? (Hint: this is a common color.)
