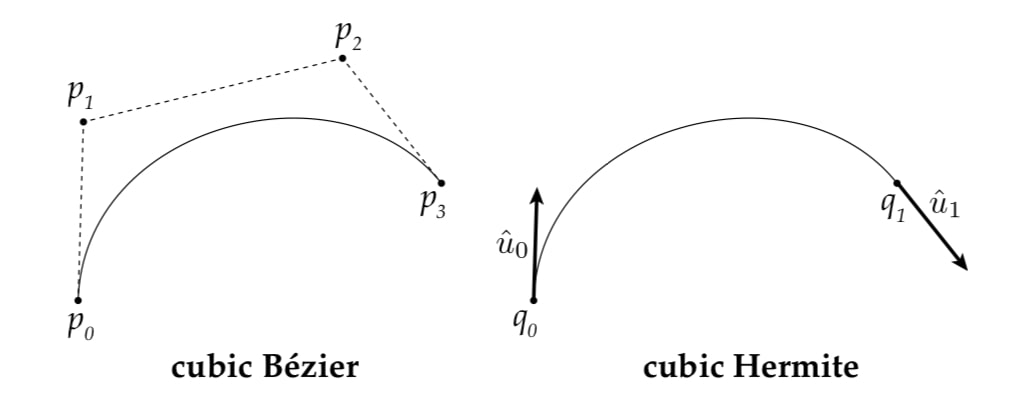
Different file formats and software systems will use different internal representations for curves. In this exercise, you'll write some basic code for converting between such representations. Two common types of curves used in 2D graphics (e.g., font rendering or illustration software) are Bezier curves and Hermite splines. A Bezier curve is specified by four control points; a Hermite curve is specified by two control points and two tangents. Actually, both of these curves are cubic polynomials. The only difference is that they are expressed with respect to different bases. In particular, a cubic Bezier curve is a linear combination of cubic Bernstein bases Bi(t), where the integer control points pi serve as constant coefficients:

p(t) = p0 * B0(t) + p1 * B1(t) + p2 * B2(t) + p3 * B3(t), t in range [0,1].

The cubic Bernstein bases are given explicitly by:

B0(t) = (1 - t)^3

B1(t) = 3 * (1 - t)^2 * t

B2(t) = 3 * (1 - t) * t^2

B3(t) = t^3

Similarly, a cubic Hermite spline is a linear combination.

q(t) = q0 * H00(t) + u0 * H10(t) + q1 * H01(t) + u1 * H11(t), t in range [0,1].

where q0 and q1 are the endpoints of the curve, u0 and u1 are the tangents at the two endpoints, and H(t) are the cubic Hermite bases.

H00(t) = (1 + 2t) * (1 - t)^2

H10(t) = t * (1 - t)^2

H01(t) = t^2 * (3 - 2t)

H11(t) = - t^2 * (1 - t)

Your task is to implement simple routines (prototyped below) that convert a cubic Bezier to a cubic Hermite curve and vice versa. Rather than hold your hand every step of the way, the purpose of this exercise is to give you some exposure to what it's like to do graphics: you have a high-level task, and you have to figure out how to break it down, formulate the right equations, solve those equations, and turn the results into code. This kind of activity is really the bread and butter of doing computer graphics. We will however give you one small hint: change of basis. :-)

Please write pseudocode and submit as a pdf.

// given coefficients for a cubic curve in Bezier form, computes the
// coefficients for an equivalent curve in Hermite form
void BezierToHermite( Vector  p0, Vector  p1, Vector  p2, Vector  p3,
                      Vector& q0, Vector& u0, Vector& q1, Vector& u1 )
{



}

// given coefficients for a cubic curve in Hermite form, computes the
// coefficients for an equivalent curve in Bezier form
void HermiteToBezier( Vector  q0, Vector  u0, Vector  q1, Vector  u1,
                      Vector& p0, Vector& p1, Vector& p2, Vector& p3 )
{



}