[This quiz is due Tuesday, September 15 at the beginning of class. Please remember to submit to Gradescope!]

A major theme of yesterday's lecture, and a major theme of our class, was how poor sampling and reconstruction can lead to aliasing.

Recall that aliasing means, roughly speaking, when something appears to be what it is not. (In English, an "alias" essentially just means a false name or identity.) In computer graphics and signal processing, aliasing occurs because of a mismatch between sampling and reconstruction: the rate or manner in which a signal is sampled is insufficient to provide a faithful reconstruction of the original signal.

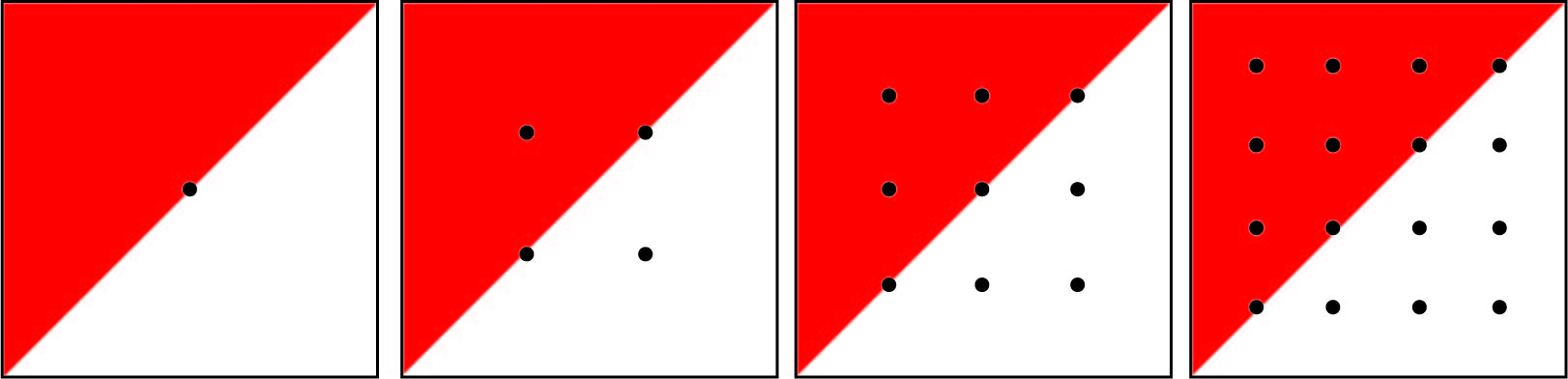
For this exercise we will be looking at how various sampling methods and resolutions can affect the reconstruction of the image. We will be using supersampling to compute the value of the same pixel. For each cell, the red triangle takes up exactly half of the pixel. If the sample is being taken at the edge of the triangle, it is counted as being inside the triangle in this example.

1. What is the percent red for each supersampled pixel? Please compute this for each of the 4 images below.

2. Plot a graph of the relative sampling error as we increase the supersample rate from 1 to 4. Recall that the relative error is abs(samplePercent - truePercent) / truePercent.

3. Based on your graph, what do you notice about the error? Does it increase or decrease in this case? What does that tell you about the pixel accuracy as we increase the supersample rate?

We just learned that increasing the sample count can help us more accurately rasterize triangles, but that is not always the case. Consider the following 4x4 supersampling pattern for a single pixel.

4. Draw a set of primitives inside the pixel that would lead to a high relative sampling error.

As you may have noticed, sampling is a difficult problem. We cannot generalize sampling to say that "taking more samples will reduce relative sampling error" since it highly depends on the primitive layout in each pixel.

Now we will explore a little bit on the time complexity of determining the coverage of a triangle. We have a 16x16 pixel grid and we take one sample per pixel. Coverage is determined by testing if the center of a pixel is inside the triangle.

5. How many pixels do we need to check?

In lecture, we breifly covered the idea of the tiled-based rasterization in modern GPUs. Say we want to determine the coverage of the triangle in the same picture as above by doing one sample per pixel again. However, now we partition the entire image into 4x4 tiles.

We give you a black-box program: tile_in_triangle, which takes in a tile and returns true iff the entire tile is in the triagle, and false iff the entire tile is outside the triangle, and partial if a tile is partialy inside the triangle. Note that this program is in constant time when given a tile and a triangle because you have a total of 3+4=7 points and 7 edges that you need to consider. We will not go into details on how this can be implemented as it is slightly more difficult, but you are more than welcome to explore on your own :)

6. How many pixel checks do we now need to perform now? (Do not count tile-checking in your total)