Now that we're done with our long, painful math review, let's see how we can use all that knowledge to actually make some beautiful images! In our vector calculus lecture, we discussed a number of different ways to think about and compute the gradient, summarized in the vector calculus slides. But for simple quantities like lengths and angles there is often a much easier, geometric way to come up with the gradient that doesn't any involve limits or partial derivatives or anything like that. We basically have to ask ourselves: what's the quickest way to make this quantity change? Here's one nice example.

If we dip a loop of wire in soapy water, we get a soap film that takes on all sorts of interesting shapes, depending on the shape of the wire:

How can we compute the shape of a soap film? One important observation about soap bubbles is that they try to minimize their total area; for this reason, they are often modeled as so-called minimal surfaces. Computationally, we might approximate a surface as a collection of triangles glued together along their edges:

But how do we push the surface toward one that has minimal area? One idea is to visit each vertex of the mesh, and move it in the direction that most rapidly reduces the surface area. Since the surface is made of triangles, our whole problem actually boils down to one simple question: for a given vertex of a triangle, how do we move it so that the triangle area shrinks as fast as possible? In other words, what is the gradient of area with respect to the position of some vertex?

Consider a triangle with vertices p, q, and r. For now you can assume these vertices live in 2D.

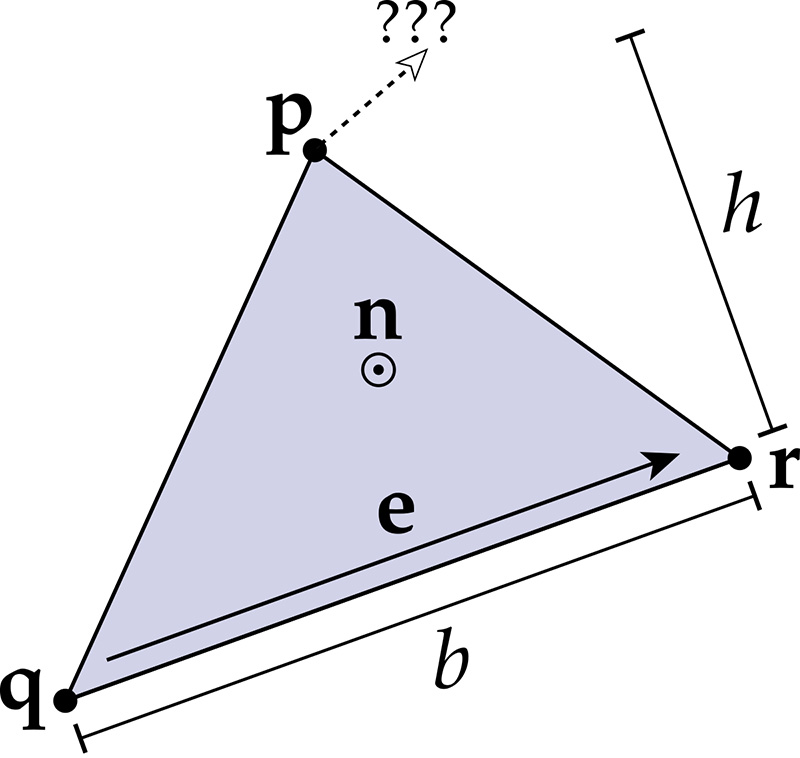
Recall that the area of a triangle is given by

A = bh/2,

i.e., the area A is one-half the base length b times the height h.

Suppose we're only allowed to move vertex p. What direction should we it so that area shrinks as quickly as possible (corresponding to the collapsing of our soap film)? To make this question easier, we can break it down into a three smaller sub-questions.

[Note: The answers you give below should not involve any coordinate calculations, cross products, determinants, or matrices. You should be able to give all the answers using simple geometric arguments like, "it gets bigger if you move it in (some direction) because of (some reason)."]

1. What direction can we move p such that the area does not change? For future reference, let's call this direction u. [Hint: think about the area formula above. Are there motions of p that change the height? Are there motions of p that change the base? Are there motions that keep these quantities the same? Etc.]
2. Since we now know the direction that doesn't change the area, we know that the fastest way to change the area is to move in the orthogonal direction, which we'll call v. (Intuitively, by moving p along v, we are not "wasting any time" by traveling along u, which doesn't change the area at all.) The next question is: how much does the area change when we move p along v? More precisely: suppose we move along v by a unit distance (in the direction that decreases area, rather than increasing it). How much does the area change? How much, therefore, does the area change per unit distance traveled? [Hint: Again, you should only have to consider the formula for the area given above.]
3. Now that you know the direction and the magnitude of the gradient, it would be useful to have a final expression for the gradient vector that can be used for numerical computation. Come up with an expression for a vector g that (i) points in the direction of quickest area decrease, and (ii) has magnitude equal to the area change per unit distance traveled. [Hint: your final expression should involve only the edge vector e := r - q, the unit normal n sticking out of the plane, and perhaps some constants and basic vector operations.]
4. Bonus Question (extra credit): So far, we have considered only motions in 2D. Can we shrink the area even faster by moving p out of the plane? Explain why or why not.

The quiz is now over. (Phew!) At this point, believe it or not, you basically know how to write some code that produces soap bubbles. The high-level procedure is

• For each vertex, compute the gradient of area using the expression you derived above.
• Move each vertex p a tiny bit in the direction of this area gradient. I.e., replace p with p + t g for some small "time step" t.
• Repeat until the triangle mesh looks like a soap bubble.

The only thing you're missing, perhaps, is some knowledge of how to work with mesh data structures---and how to draw the result on the screen! We'll take a look at all of these questions in lectures throughout the semester.