[Due at the start of class on Wednesday, November 15.]

After graduating, you decide to start a company that makes color-changing lightbulbs that can be controlled via smartphone app. (Believe it or not, this product actually exists already!). Your basic idea is to have a red, green, and blue LED, each of which is "dimmed" by just the right amount to make the desired color. Old incandescent lightbulbs could be "dimmed" by just increasing or decreasing the voltage. However, LED lights must be either "all on" or "all off" at any given moment. A technique used to simulate dimming of LED lights (called "pulse width modulation") is to rapidly turn an LED on and off at a rate faster than the human eye can perceive. In LEDs currently on the market, the light is turned off and on at regular intervals. Your company hopes to gain a competitive advantage with a new design where the light gets turned off and on randomly, to avoid any potential aliasing. However, you first have to do a few calculations to figure out how to properly control the color.

Expected Color of an LED

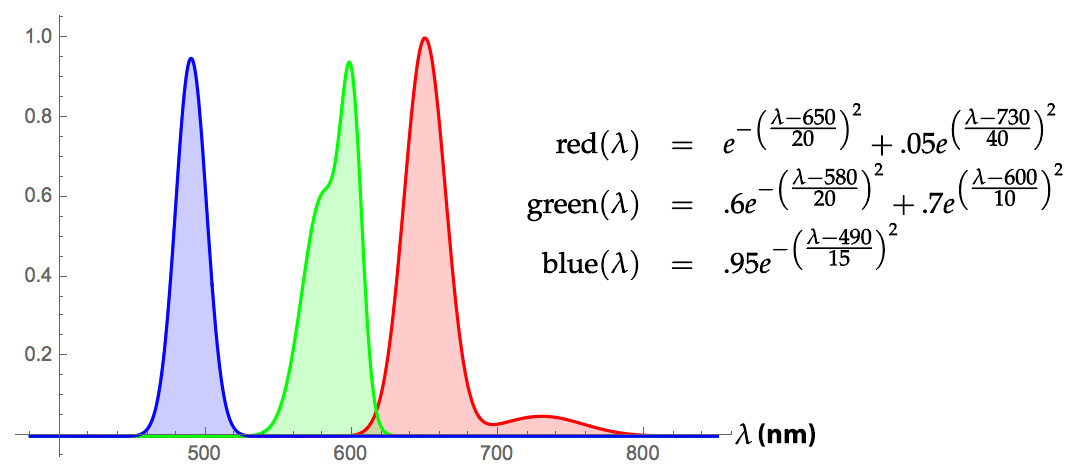
Each color of LED has a narrow but still somewhat complicated emission spectrum, given above. To make life easier, let's summarize each of these spectra by their expected wavelength. In this case, we can compute the expected wavelength of a spectrum f as

(Where does this formula come from? Basically we've just normalized the spectrum by its total, so that it's a probability distribution, and then integrate "wavelength times probability"). Using this formula, numerically estimate the average wavelength for each color of LED, using any method we discussed in the lecture on numerical integration. You can assume that it's sufficient to integrate over visible wavelengths. We strongly recommend you write a little piece of code to do this, but you do not have to turn in your code.

Round your result to the nearest integer (in nm).

What color do we see?

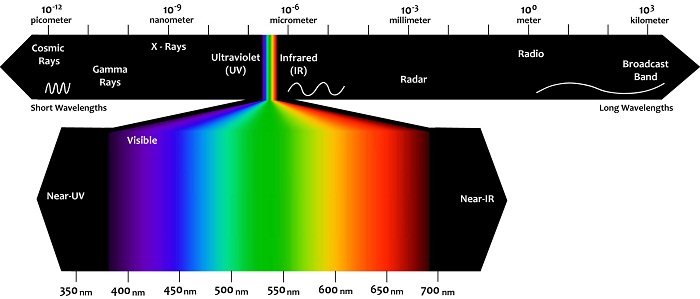
Suppose the three lights get switched on with the probabilities given below. Using the three wavelengths computed in your previous answer as a proxy for the wavelength of each LED, what is the expected wavelength of the observed light? Roughly what color does this correspond to?

Round your result to the nearest integer (in nm).

pRed = 0.6

pGreen = 0.3

pBlue = 0.1

How much does the color flicker?

Your customers like the new light bulb design, but are worried that the color of the light will jump around, due to the different LEDs being randomly switched off and on. Using the same probabilities as in the previous part, compute the standard deviation of the wavelength that will be observed, i.e., the square root of the variance. How could you build a lightbulb with less variance in color?

Round your result to the nearest integer (in nm).