[Note: not all quiz questions will be this long! But hopefully you have fun with this one. :-) Remember: quizzes are graded entirely on effort; we care far more that you learn and grow than we do about the final answer! As with all quizzes, please write/print your answer on a piece of paper, to be turned in at the beginning of next lecture.]
In class, we discussed a number of different ways to think about and compute the gradient. But for geometric quantities (like lengths and angles in 2D or 3D) there is often a much easier, geometric way to come up with the gradient that doesn't any involve limits or coordinate calculations at all. Here's one example.
If we dip a loop of wire in soapy water, we get a soap film that takes on all sorts of interesting shapes, depending on the shape of the wire:

How can we compute the shape of a soap film? One important observation about soap bubbles is that they try to minimize their total area; for this reason, they are often modeled as so-called minimal surfaces. Computationally, we might approximate a surface as a collection of triangles glued together along their edges:

But how do we push the surface toward one that has minimal area? One idea is to visit each vertex of the mesh, and move it in the direction that most rapidly reduces the surface area. Since the surface is made of triangles, our whole problem actually boils down to one simple question: for a given vertex of a triangle, how do we move it so that the triangle area shrinks as fast as possible? In other words, what is the gradient of area with respect to the position of some vertex?
Consider a triangle with vertices $\mathbf{p},\mathbf{q},\mathbf{r} \in \mathbb{R}^3$:
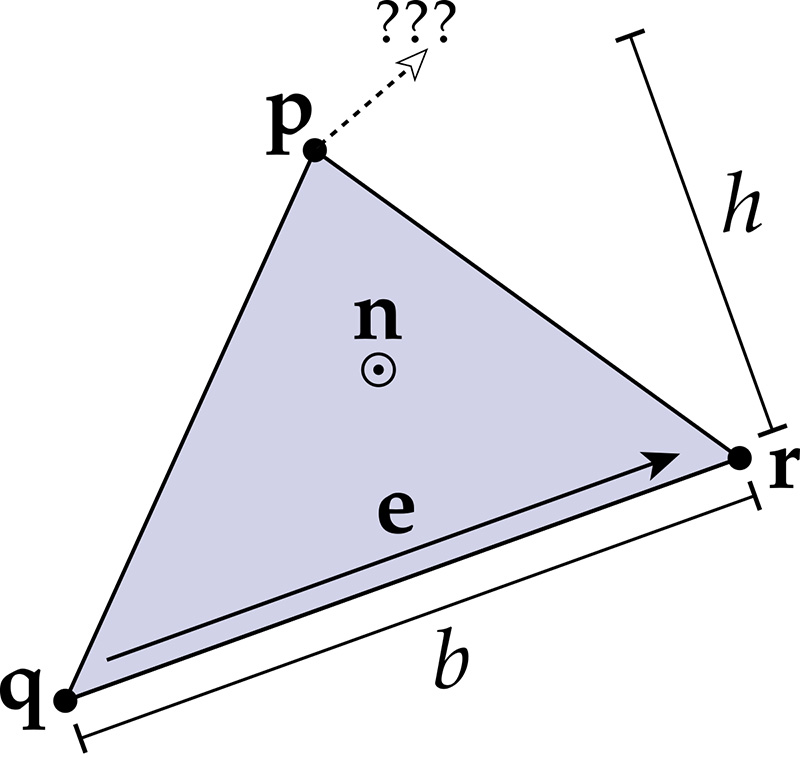
Suppose we pick one of the vertices, say, $\mathbf{p}$. What direction should we move $\mathbf{p}$ to reduce the area as quickly as possible? We can further simplify this question by breaking it down into a few smaller sub-questions. At this point, it's probably wise to recall the formula for the area of a triangle:
$$A = \tfrac{1}{2}bh.$$
In other words, the area $A$ is one-half the base length $b$ times the height $h$.
[Note: The answers you give below should not require any coordinate manipulations, cross products, determinants, or matrices; you should need only simple geometric arguments that can be expressed in (more or less) plain English prose.]
- Suppose that for now we just think about sliding $\mathbf{p}$ around in the 2D plane containing the triangle. What direction can we move $\mathbf{p}$ such that the area does not change? For future reference, let's call this direction $\mathbf{u}$. [Hint: think about the area formula above. Are there motions of $\mathbf{p}$ that change the height? Are there motions that keep the height the same? Is it possible to change the base length? Etc.]
- Since we now know the direction that doesn't change the area, we know that the fastest way to change the area is to move in the orthogonal direction, which we'll call $\mathbf{u}^\perp$. (Intuitively, by moving $\mathbf{p}$ along $\mathbf{u}^\perp$, we are not "wasting any time" by traveling along the direction $\mathbf{u}$, which doesn't change the area.) The next question is: how much does the area change when we move $\mathbf{p}$ along $\mathbf{u}^\perp$? More precisely: suppose we move along $\mathbf{u}^\perp$ by a unit distance (in the direction that decreases area, rather than increasing it). How much does the area change? How much, therefore, does the area change per unit distance traveled? [Hint: Again, you should only have to consider the formula for the area given above.]
- Now that you know the direction and the magnitude of the gradient, it would be useful to have a final expression for the gradient vector that can be used for numerical computation. Come up with an expression for a vector $\mathbf{g}$ that (i) points in the direction of quickest area decrease, and (ii) has magnitude equal to the area change per unit distance traveled. [Hint: your final expression should involve only the edge vector $\mathbf{e} := \mathbf{r} - \mathbf{q}$, the unit normal $\mathbf{n}$ pointing out of the triangle, and perhaps some constants and basic vector operations.]
- Bonus Question (worth 0 extra credit points): So far, we have only considered in-plane motions of the point $\mathbf{p}$. Couldn't there be a way to shrink the area even faster by moving $\mathbf{p}$ out of the plane? Explain why out-of-plane motions do not help us shrink the area of our triangle. [Hint: if we rigidly rotate a triangle, what happens to its area?]
At this point, believe it or not, you more or less know how to write some code that produces bubbly surfaces. The high-level procedure is
- For each vertex, compute the gradient of area using the expression you derived above.
- Move each vertex $i$ a tiny bit in the direction of this area gradient. I.e., replace $\mathbf{p}_i$ with $\mathbf{p}_i + \varepsilon \mathbf{g}_i$.
- Repeat until the surface looks like a soap bubble.
The only thing you're missing, perhaps, is some knowledge of how to work with mesh data structures---and how to draw the result on the screen! We'll take a look at all of these questions in lectures throughout the semester.