In your last quiz, you figured out how to draw a tree by recursively applying spatial transformations. Drawing a 3D tree is really no different, except that you now want to apply 3D rotations, translations, and rescalings:

Suppose now that we want to plant this tree all over a little planet:

In computer graphics, this kind of duplication is called "instancing." The only question is, how do we find the transformation that takes a tree from one place on the planet to another? In particular, suppose that you have a tree made of up of a set of points ${\mathbf{q}_1, \ldots, \mathbf{q}_n}$ sitting on top of a triangle with vertices $(\mathbf{p}_1, \mathbf{p}_2, \mathbf{p}_3)$:

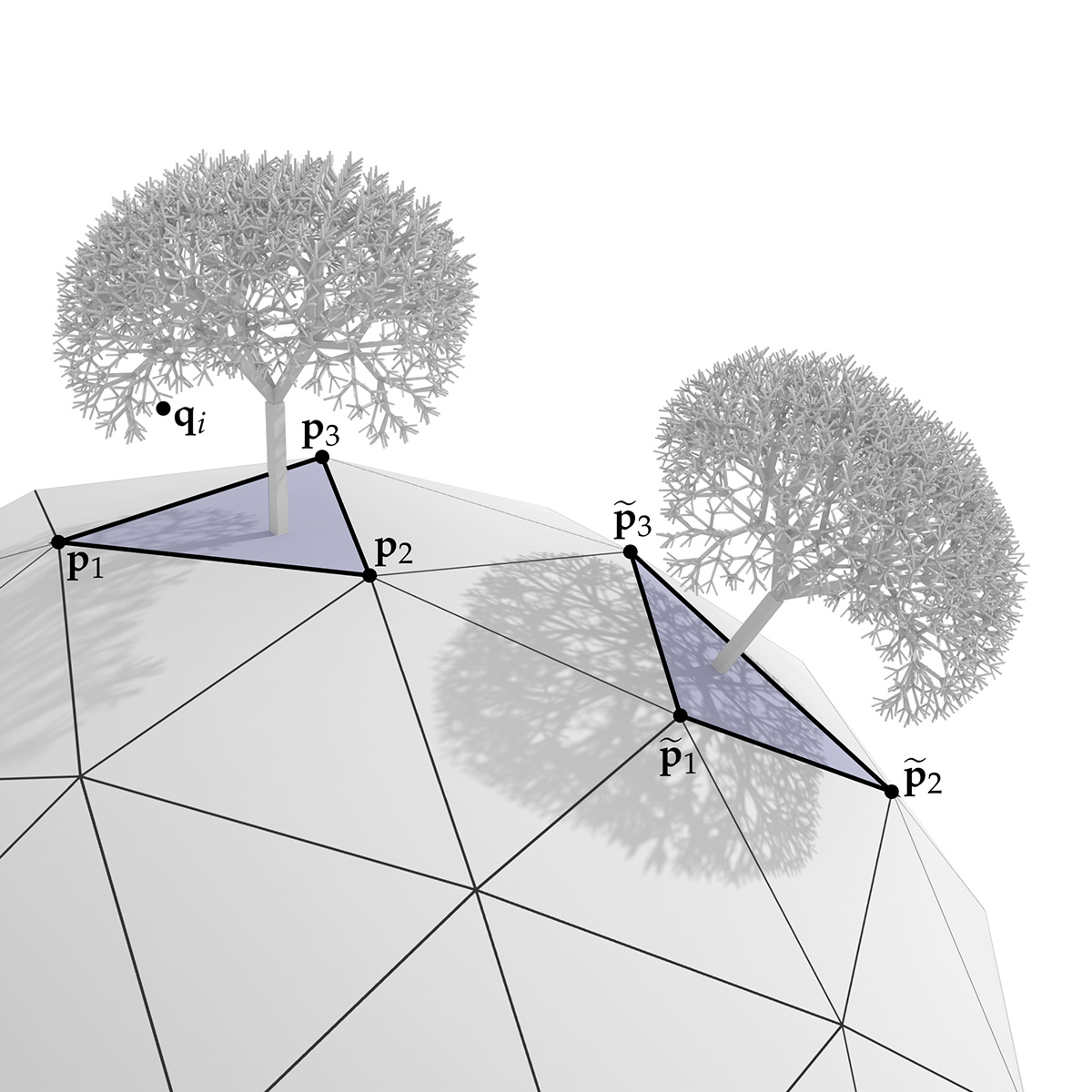
You want to plant a new tree on triangle $(\widetilde{\mathbf{p}}_1, \widetilde{\mathbf{p}}_2, \widetilde{\mathbf{p}}_3)$.

1. Describe, at a very high level in words (no math) how you might go about finding a transformation that takes the points $\mathbf{q}_i$ to their new locations over the target triangle.
2. Give any formula (in terms of the vertex positions) for a 3D rotation that rotates the source triangle such that it is parallel to the target triangle. Be careful about orientation---for instance, you don't want to stick the top of the tree into the ground!

As you hopefully outlined in part (1), the rotation alone isn't enough to determine how to transform the tree, though it is perhaps the hardest part. Bonus question (worth 0 points): how do you compute the rest of your transformation?

Note: there is not just one answer to this question! There are many possible rotations, which can be expressed in many ways. For instance, you could use an axis-angle representation. Or quaternions. Or you could attempt to use Euler angles (ha!). Or you could think about constructing orthonormal bases associated with both triangles. One thing to keep in mind: is this rotation uniquely determined? And how do I pick a rotation if it's not?